O zmienności w czasie modułów sprężystości podłużnej E i poprzecznej G oraz ich wpływie na sztywność konstrukcji z drewna

Barbara Misztal

doi:10.37190/arc250311

Streszczenie

W artykule sformułowano problem braku analizy zmian sztywności w czasie wielkoprzestrzennych konstrukcji z drewna klejonego, opisując kopułę Konohana Dome w Japonii. Na przykładzie badań belki z drewna sosnowego o schemacie statycznym wspornika wykazano, że pomiar ugięć pozwala oszacować sztywność sprężystą i postaciową modelu badawczego. Udowodniono także, że wraz ze wzrostem ugięć w czasie zmniejszają się moduły sprężystości podłużnej E i poprzecznej G. Ujawniono, że przyczyną nieliniowego przyrostu ugięć w czasie jest malejąca sztywność sprężysta i postaciowa belki wspornikowej.

Słowa kluczowe

moduł sztywności podłużnej, moduł sztywności poprzecznej, siła krytyczna, sztywność konstrukcji

Podgląd pełnego artykułu jest możliwy wyłącznie na większych ekranach.

2025

3(83)

Barbara Misztal*

On the variability in time of the longitudinal modulus

of elasticity E and the traverse modulus of elasticity G

and their impact on the rigidity of timber structures

DOI: 10.37190/arc250311

Published in open access. CC BY NC ND license

Abstract

The paper formulated the problem of lack of analysis of changes in rigidity over time, large-space constructions of glued wood, describing the dome

of Konohana Dome in Japan. On the example of a study of pine beams with a static support scheme, it was shown that on the basis of the bending mea-

surement it was possible to estimate the spring and form rigidity of the research model. It has been shown that with the increase in bending over time,

the moduli of longitudinal E and transverse G elasticity decreases. It has been revealed that the cause of the nonlinear increase in bending over time is

the decreasing rigidity of the spring and the shape of the support beam.

Key words: modulus of longitudinal rigidity, modulus of transverse rigidity, critical force, structural rigidity

Introduction

The building industry of glued wood has developed

dynamically since the forties of the 20

century, since the

development and implementation on industrial scale of

water-proof resorcinol glues on the basis of resins (RPF).

Since the seventies of the 20

century large-capacity facil-

ities having the function of sports and spectators halls have

been built. One of the examples is the little-known in Eu-

rope the multi-function spectators hall, Konohana Dome, at

Miyazaki in Japan. In the Polish and global references no

analysis in time of the rigidity of the construction of such

facilities has been found. Referring to the study by Zbig-

niew Kowal (1996) and using the analogy of the structure

of wood to the building of brous composites, the author

of this paper has conducted her own experiment, reveal-

ing that on the basis of the measurement of deections it is

possible to assess the tendency of variations in time of the

rigidity of wooden constructional elements and systems.

Description of the research problem

The large-spatial dome, Konohana Dome (Fig. 1), was

built in 2004 of glued wood (Iimura 2008). The facility

constitutes a big achievement in the eld of architecture,

building technology and construction. Bars of glued wood

were used therein, including thickset bars of a slimness of

λ < 20, connected with steel knots. The steel knots were

connected with wooden bars using steel sheets glued into

the wooden section. Despite noticing a range of negative

processes in such constructions, e.g., the increase in de-

ections of wooden elements in time without a rise in the

load, appearing, among others, in the dome at Portland,

USA (Misztal 2018), and the ssion of the bres of wood-

en bars in the zones at by steel nodes (Lachiewicz-Złotow-

ska, Orłowicz 2008), no recognition research is conducted

within the eld of a change in the rigidity of construction

wooden systems study in time.

The shape of the Konohana Dome was built with wood

glued in layers from December 2002 until March 2004. The

bars of the cantilever structure of a section 30 × 120 cm was

made of the quickly-growing tree: Japanese cryptomeria

(Sekkan-sugi, Cryptomeria japonica), appearing in the vi-

cinity of the city of Miyazaki, growing for at least 40 years

* ORCID:

0000-0001-7811-1331. Faculty of Architecture, Wrocław

University of Technology, Poland, e-mail: barbara.misztal@pwr.edu.pl

116 Barbara Misztal

since after that time the sugi wood gets the strength su-

cient to make the construction.

The dome having an elliptic shape of the horizontal projec-

tion has a diameter inside the projection of 122.0 ×

104.5 m

and the greatest height of 38.0 m. The total area of the pro-

jections amounts to 10,966.0 m

. The volume of the glued

wood, of which the wooden structure was made, amounts to

1,381.0 m

. The mass of the wooden structure as converted

into 1 m

of the projection, totals 42.80 kg/m

whereas the

mass of the steel, of which the knots were made (Figs. 1c, d)

and the steel structure that tightens the fabric constituting

the outside shell totals 44.70 kg/m

(Iimura 2008).

The construction of the dome is a steel-wood beam scaf-

folding having a double curvature. Such a system is an

arrangement of wooden bars susceptible to the action of

transverse forces in the sections by the steel knots, espe-

cially in thickset bars of a small slimness (Fig. 1d). In the

paper, Strength Performance of Glulam Made of Obi-sugi

Laminae with Low Young’s Modulus of Bending (Matsu-

moto et al. 2007), the method of determining the modulus

of elasticity E of sugi wood, of which the structure of the

dome at Miyazaki was described, however, the modulus of

transverse elasticity G was not determined. The variations

in time of the moduli of longitudinal elasticity E and that of

transverse elasticity G was not examined.

The domes made of glued wood, including the dome

at Miyazaki, are made of the natural brous composite, as

wood is. The brous composites behave, unlike homog

enous materials, such as steel. Kowal (1996) introduced

a model of the theoretical analysis of constricted composite

bars. When examining them, he found that the

shape of the

bar destruction depended on the bar slimness,

the properties

of bres and the matrix as described by the moduli of longi-

tudinal elasticity E and transverse elasticity G

as well as on

the value of the quotient E/G. Kowal discovered the para-

dox of the load carrying-capacity of composite bars: thick-

set composite bars of the slimness of λ < 20

show a lower

critical load capacity than those of a higher slimness, e.g.,

λ > 80. The graphs compiled by the author of the paper

(Misztal 2018) on the basis of the results of the study by

Fig. 1. Beam scaffolding, steel-wood Konohana Dome built with sugi wood in Miyazaki, Japan, 2004:

a) location of the Konohana Dome, b) view of the dome from the entrance side, c) view of the wooden structure from the inside,

d) view of the steel knot and constricted wooden bars in the support zone of the dome structure (photo by B. Misztal)

Il. 1. Ruszt belkowy, stalowo-drewniany kopuły Konohana Dome wybudowanej z drewna sugi w Miyazaki, Japonia, 2004:

a) lokalizacja kopuły, b) widok kopuły od strony wejścia, c) widok konstrukcji drewnianej od wewnątrz,

d) widok stalowego węzła i krępych prętów z drewna w strefie podporowej konstrukcji kopuły (fot. B. Misztal)

b d

On the variability in time of the longitudinal modulus of elasticity E and the traverse modulus of elasticity G 117

Kowal presents how grows the coecient decreasing the

load capacity η for bars of a slimness of λ < 20 (Fig. 2).

The coecient η is important since it tells us, how many

times the critical load-bearing capacity of a constricted bar

decreases depending on the slimness λ and on the relation

E/G according to the equation by Kowal.

Since wood is a natural brous composite, similar phe-

nomena should be expected as in articial brous com

pos-

ites. For these reasons the author of the paper has been deal-

ing, for many years, with the exploration of wood as a b

rous

composite, including the moduli of elasticity of wood.

In the referenced literature of this subject matter no re-

search by other authors has been noticed about a change in

time of the moduli of elasticity E and G of wood, as well as

on the critical load-bearing capacity of wooden structures

as well as the variations of their rigidity in time.

Considering the impact of wood (as reected by the mag

nitudes of E and G) on the aesthetics, durability and safety

of the facilities made of wood, the author of the paper con-

ducted her own experiment in order to show how changes

the value of the moduli of elasticity of wood in time. The

information on the moduli of elasticity, both longitudinal E

and transverse ones G, has the basic meaning for the devel-

opment of the large-spatial facilities made of glued wood,

the assessment of the rigidity and the load-bearing capacity

in time. The knowledge of the magnitudes of E and G pro-

vides a possibility to forecast in time the variations of an ar-

chitectonic form and the load-bearing capacity of a structure.

The objective of the research

The objective of the research conducted by the author of

this paper is to show that:

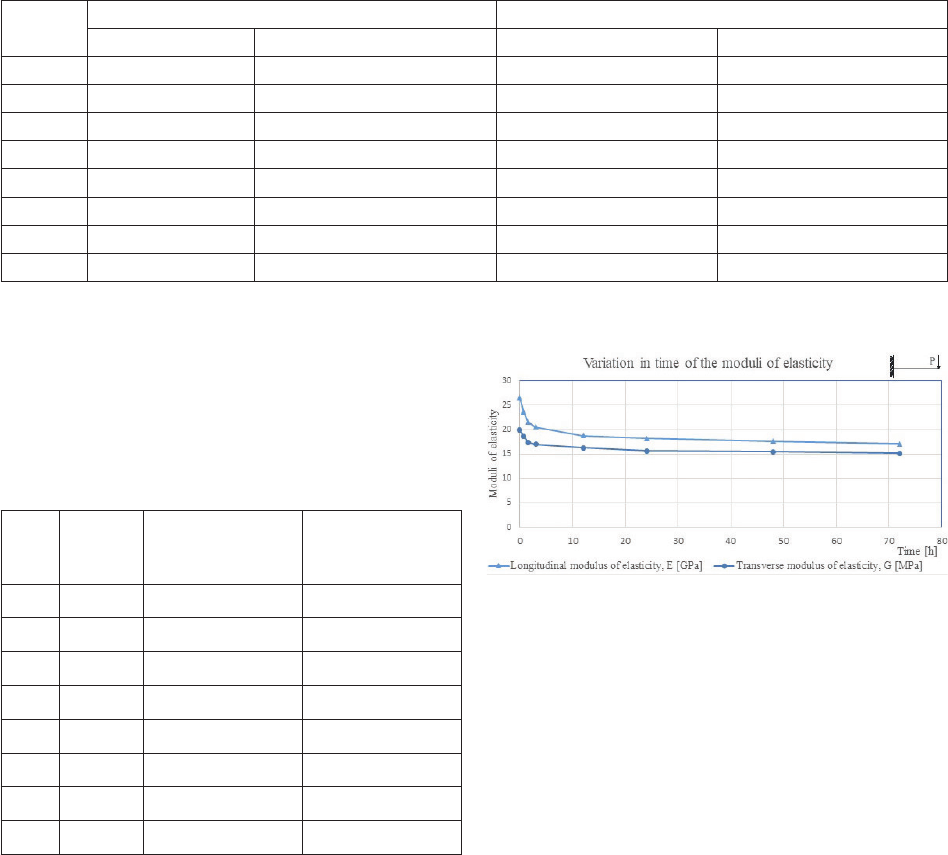
1. The tendency of the variations of the moduli of trans-

verse rigidity G and that of longitudinal elasticity E can be

diagnosed on the basis of the measurements of deections.

2. The rigidity of a wooden element changes in time.

Description of own research

Theoretical basics of the method

The author of the paper has dealt for many years with

the theoretical basics of the research about the moduli of

longitudinal elasticity and that of transverse elasticity. In

her publication dated 2020 (Misztal 2020), she specied

the algorithm to determine the values of longitudinal elas-

ticity E and that of transverse elasticity G, as well as she

examined the model of a spruce wood beam. Reminded in

this paper is the course of calculations of the moduli E and

G, in order to prove that the rigidity of a wooden element

varies in time. To this aim, the author of the paper conduct-

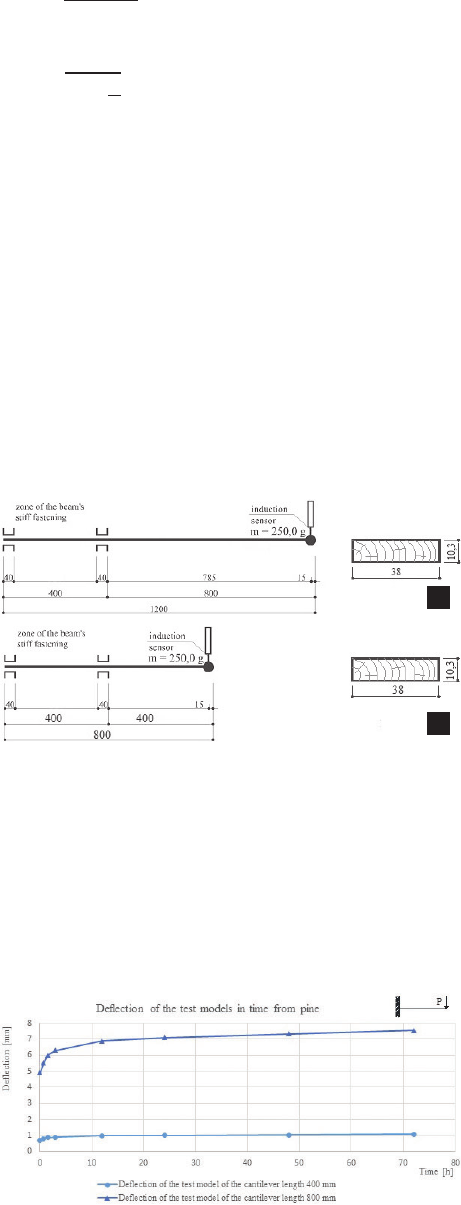
ed an experiment on two models of a cantilever beam made

of pine wood.

In the research scheme adopted for the research the

total deection of the supporting beam depends on the

bending rigidity EJ and on the shape rigidity FG of the bar

(E – modulus of longitudinal elasticity, G – modulus of

transverse elasticity, J – moment of inertia of the bar sec-

tion, F – cross-sectional area of the bar).

An experiment lasting for 72 hours was scheduled. The

examination of two cantilever beams having the length of

= 2l

and l

was conducted (2). The system of equations

(3) and (4) was arranged:

For the cantilever beam of the lenght l

= 800 mm, where

= 2l

(2)

(3)

For the cantilever beam of the lenght l

= 400 mm:

(4)

Cantilever beam’s cross-section:

Geometric moment of inertia of the cantilever beam’s

cross-section:

The coecients designated as A were introduced

– equation (5) and B – equation (6) (5)

(6)

Fig. 2. Graph of the reduction factor η for the critical load-bearing

capacity of compressed members according to equation (1)

(elaborated by Misztal 2018)

equation (1):s ssssssssss ss

– critical load of the composite member, N

– Euler’s critical load,

η – reduction factor for the Euler-based critical load according to

classical mechanics (source: Kowal 1996)

Il. 2. Wykres współczynnika η zmniejszającego nośność krytyczną

prętów ściskanych według wzoru (1) (oprac. Misztal 2018)

wzór (1): cc cc

– siła krytyczna pręta kompozytowego,

– siła krytyczna według Eulera,

η – współczynnik zmniejszający siłę krytyczną liczoną z wzoru Eulera

według zasad mechaniki klasycznej (źródło: Kowal 1996)

























3





8

3

2







3





 = 3.8 × 1.03 × 10

−4

= 3.914 × 10

−4

 =

3.8 × 10

−2

[

]

(

1.03 × 10

−2

[

]

)

= 0.3460302 × 10

−8

 =

3.8 × 10

−2

[

]

(

1.03 × 10

−2

[

]

)

= 0.3460302 × 10

−8

 =



3

2.50×

(

40 × 10

−2

)

3 × 0.3460302 × 10

−8

= 15412912.9 [

]

 =



3

2.50×

(

40 × 10

−2

)

3 × 0.3460302 × 10

−8

= 15412912.9 [

]

 =





2.50× 40 × 10

−2

3.914 × 10

−4

= 2554.9 [

]

118 Barbara Misztal

The solution for the system of equation (3) and (4) are

equations (7) and (8)

, A – equation (5) (7)

, A – equation (5) and B – equation (6) (8)

The formulae for the accounting determination of the

values of the modulus of longitudinal elasticity E and that

of transverse elasticity G using the measured deections of

the model of the cantilever beam were obtained.

Research

Selected for the research were beams made of pine wood

in an air-dry state. The experiment was conducted in a room

of a temperature of 22°C and a humidity of ca. 40%. The

measurements of deections were performed on the free

end of the cantilever using an inductive sensor connected to

a computer on which the values of deections were recorded:

immediately upon the experiment for the time t

= 0.00, af-

ter the time t

= 0.75 hours, t

= 1.50 hours, t

= 3.00 hours,

= 12.00 hours, t

= 24.00 hours, t

= 48.00 hours, t

= 72.00

hours.

The rst research model had the following dimensions:

the cross-section of 1.03 × 38 mm, the length of 1,200 mm,

the second research model: cross-section 1.03 × 38 mm,

length 800 mm. The models were weighed before the ex-

periment. Considering a tiny mass, the own mass of the

models was omitted. Fastened on the rst research model,

on one end, was the model of the cantilever beam accord-

ing to the schematic shown in Figure 3a, having the length

of the cantilver of 800 mm.

The load of the value of m = 250 g was applied on the

free end of the cantilever perpendicularly to the plane of

the lower rigidity of the beam. The temporary deection

was measured immediately, which amounted to y

= 4.91

mm = 4.91 × 10

–3

m. After the time t

= 0.75 hours of the

impact of the deection was read out: it amounted to y

5.50 mm = 5.50 × 10

–3

m. The successive deections were

measured over the time of 72 hours of the experiment’s du-

ration and were listed in Table 1. The graph of the deec-

tions measured was shown in Figure 4.

Prepared for testing on the second test stand was another

model having the static schematic, as shown in 4a, of the

cantilever length of l

= 400 mm. The beam was fastened

on one end, whereas the another, free end was loaded with

a concentrated mass m = 250 g perpendicularly to the plane

of the lower rigidity of the beam, as shown on the schematic

in Figure 3b.

Immediately upon suspending the mass m = 250 g, the

temporary deection was measured in time t

= 0.00, the

temporary deection measured amounted to y

= 0.71 mm

= 0.71 × 10

–3

m. After the time t

= 0.75 hours, the im-

pact of the load was re-read, the impact of the deection

amounted to y

= 0.79 mm = 0.79 × 10

–3

m. Successive de-

ections were read out in the time of 72 hours and listed in

Table 1. The graph of the deections measured in function

of time is shown in Fig. 4.

Results of the testing

Listed in Table 1 are the deections measured during

72 hours of the experiment’s duration.

The total increase in deections of the model a cantile-

ver length of l

= 2l

= 800 mm during 72 hours amounted

to 2.64 mm, whereas that of the model of the cantilever

length l

= 400 mm amounted to 0.36 mm. The increases in

the deections decreases in time, however, no stabilization

of deections during 72 hours of the experiment’s duration

were noticed.

While substituting the magnitudes of the deections on

the free ends of the cantilevers as listed in Table 1 and as

shown in Figure 5 to the formulae (8) and (9), calculated

were the moduli E (formula 7) and formula G (formula 8)

of the pine-wood beam tested in the dry-air state. Listed in

Table 2 are the calculated values of the moduli, whereas

shown in Figure 5 is the graph of the decreasing of the val-

ues of the modulus of elasticity E and that of the modulus

of transverse rigidity in G in time.

Fig. 4. Time-dependent deection of the free ends

of pine wood cantilevers (Fig. 3) during a 72-hour test

(elaborated by B. Misztal)

Il. 4. Zmiana w czasie ugięć swobodnych końców wsporników

z drewna sosnowego (Il. 3) w czasie próby trwającej 72 godzin

(oprac. B. Misztal)

Fig. 3. Model of the tested beam with cantilever length:

a) l

= 800 mm, b) l

= 400 mm

(schematic for dynamic testing and cross-section)

(elaborated by B. Misztal)

Il. 3. Model testowanej belki o długości wspornika:

a) l

= 800 mm, b) l

= 400 mm

(schemat belki do badań dynamicznych i przekrój)

(oprac. B. Misztal)

 =

6



− 2

 =





−





On the variability in time of the longitudinal modulus of elasticity E and the traverse modulus of elasticity G 119

Fig. 5. Time-dependent changes in the modulus of longitudinal

elasticity E and modulus of transverse rigidity G

of pine wood cantilevers (Fig. 3)

during a 72-hour test

(elaborated by B. Misztal)

Il. 5. Zmiana w czasie modułów sprężystości podłużnej E

i sztywności poprzecznej G

wsporników z drewna

sosnowego (il. 3)

w czasie próby trwającej 72 godzin

(oprac. B. Misztal)

Time

Model of the cantilever length 800 mm Model of the cantilever length 400 mm

time [h] deflection [mm] time [h] deflection [mm]

0.00 4.91 0 0.71

0.75 5.50 0.75 0.79

1.5 6.00 1.5 0.86

3 6.30 3 0.90

12 6.90 12 0.98

24 7.10 24 1.01

48 7.33 48 1.04

72 7.55 72 1.07

Table 1. Chart of deflections in function of the time measured during 72 hours of the experiment (elaborated by B. Misztal)

Tabela 1. Wartości ugięć w funkcji czasu zmierzonego w ciągu 72 godzin doświadczenia (oprac. B. Misztal)

Time

[h]

Longitudinal

modulus of elasticity

E [GPa]

Transverse

modulus of elasticity

G [MPa]

0 26.49 19.91

0.75 23.59 18.69

1.5 21.60 17.42

3 20.55 17.03

12 18.79 16.31

24 18.20 15.64

48 17.61 15.48

72 17.09 15.18

Table 2. List of modules of longitudinal rigidity

and transverse rigidity G of tested beams

(elaborated by B. Misztal)

Tabela 2. Zestawienie modułów sztywności

podłużnej i sztywności poprzecznej G

badanych belek wspornikowych

(oprac. B. Misztal)

Summary

The knowledge of the magnitudes of the longitudinal

elasticity E and that of the transverse elasticity G as well

as that of their variations in time has the meaning for the

further development of wooden constructions, including

glued wood. It allows to assess the load-carrying capacity

of a construction and the deformation of architectonic forms

in time. In the experiment conducted, the deections of the

loaded cantilevers increased in time and no stabilization of

the deections after 72 hours of the experiment’s duration

was noticed. It was demonstrated in this paper that on the

basis of the measurements of deections it was possible to

assess the magnitudes of the moduli of longitudinal elastici-

ty E and that of transverse elasticity G, as well as that those

values decrease jointly with the rise in deections in time.

The cause for the non-linear increase in deections

in time is the decreasing rigid elasticity EJ and shape ri

gidity FG of a beam made of pine-wood (J – moment of

cross-sectional inertia, F – cross-section of the beam). The

fact of decreasing the rigidity of wooden elements in time

requires a further recognition, especially for large-spatial

facilities made of glued wood.

The EC5 Standard considers the variability of deec-

tions and the strength of wood in time through the coe-

cient k

mod

, depending on the class of usage and that of last

duration. However, both testing as well as the recognition

of the variability of moduli and their strength in time shall

be further deepened since they also depend on the features

of the wood being a natural brous composite. The issue

is important, especially in the case of introducing on the

market of articial composites using wood.

Translated by

Wojciech Mühleisen

120 Barbara Misztal

References

Iimura, Yutaka. “Performance Evaluation of the Konohana Dome built

with Fast-Growing Sugi.” In World Conference on Timber Engineer-

ing, Miyazaki, 2–5 June 2008, Engineered Wood Products Associa-

tion, 2008.

Kowal, Zbigniew. “Kompozytowe pręty ściskane zbrojone podłużnie

i spi ralnie.” In Problemy naukowo-badawcze budownictwa. XLII Kon-

ferencja Naukowa Komitetu Inżynierii Lądowej i Wodnej PAN i Ko mi-

tetu Nauki PZITB, Kraków-Krynica, 1996. Vol. 2. Politechnika Kra-

kowska, 1996.

Lachiewicz-Złotowska, Agata, and Roman Orłowicz. “Zachowanie się

stref przypodporowych dźwigarów łukowych i belkowych z drewna

kle jonego.” Czasopismo Techniczne. Budownictwo, no. 104 (2007):

99–106.

Matsumoto, Akihiro, Morita Hideki, Fujimoto Yoshiyasu, Shiiba Atsushi,

Iimura Yutaka. “Strength Performance of Glulam made of Obi-sugi

Laminae with low Young’s Modulus of Bending.” In 2007 IUFRO All

Division 5 Conference, Taipei, October 29–November 2, 2007, Tapei.

Miyazaki Prefectural Wood Utilization Research Center, 2007.

Misztal, Barbara. “O występowaniu i wpływie na trwałość konstrukcji

drew nianych, zmiennego w czasie modułu sztywności poprzecznej G.”

In Dziedzictwo architektoniczne. Ochrona i badania obiektów zabytko-

wych, edited by Ewa Łużyniecka. Ocyna Wydawnicza Politechniki

Wrocławskiej, 2020.

Misztal, Barbara. Wooden Domes. History and Modern Times. Springer,

2018. https://doi.org/10.1007/978-3-319-65741-7.

Streszczenie

O zmienności w czasie modułów sprężystości podłużnej E i poprzecznej G

oraz ich wpływie na sztywność konstrukcji z drewna

W artykule sformułowano problem braku analizy zmian sztywności w czasie wielkoprzestrzennych konstrukcji z drewna klejonego, opisując kopułę

Konohana Dome w Japonii. Na przykładzie badań belki z drewna sosnowego o schemacie statycznym wspornika wykazano, że pomiar ugięć pozwala

oszacować sztywność sprężystą i postaciową modelu badawczego. Udowodniono także, że wraz ze wzrostem ugięć w czasie zmniejszają się moduły

sprężystości podłużnej E i poprzecznej G. Ujawniono, że przyczyną nieliniowego przyrostu ugięć w czasie jest malejąca sztywność sprężysta i posta-

ciowa belki wspornikowej.

Słowa kluczowe: moduł sztywności podłużnej, moduł sztywności poprzecznej, siła krytyczna, sztywność konstrukcji