Delineation of buildings at Machu Picchu by Inca builders – is metrological analysis of building outlines possible without the invasive survey?

Anna Kubicka-Sowińska

doi:10.37190/arc230404

Abstract

The metrological analysis of the Inca architectural elements at Machu Picchu using the cosine quantogram method was preceded by tests of different models of building delineation and erection, which aim to test the method’s effectiveness in detecting the quantum with a differently defined error occurring in the survey sample. The sources of such errors may lie in the work of Inca builders and the modern researcher. The measurements of the architectural elements represent data from 3D laser scanning. The data obtained in this way refer to length measures that may have been delineated using quantum: building outlines, dimensions and distribution of doorways, windows and niches. However, it is uncertain which of them were actually planned by the Inca builders using the measure we are looking for (quantum) and which are incidental or outcome values. Due to the sloping of the external walls towards the inside of the building, which was characteristic feature of Inca architecture, and the way in which the buildings were planned (on horizontal terrain, sloping terrain or with projection onto the ground), the level at which the building is available for measurement also has an important influence on the results of the analyses. This may be analogous to the level at which the building was planned, or it may be significantly above that level. As a result of these factors, the group of tests concerns theoretically predictable combinations of the ways in which the Inca buildings were delineated and the level available for measurement. Tests of the effectiveness of the cosine quantogram method for Inca building outlines have shown that if they were laid out using some fixed measure (quantum) then, regardless of how the building was delineated: levelled terrace, sloping ground, projection from level to sloping ground, the cosine quantogram method must reveal its existence.

Full article view is only available on bigger screens.

2024

1(77)

Anna Kubicka-Sowińska*

Delineation of buildings at Machu Picchu by Inca builders

– is metrological analysis of building outlines possible

without the invasive survey?

Introduction

Research on Inca metrology with the example of ana-

lysing the architecture of Machu Picchu has been inspired

by Professor Jacek Kościuk, who shared with students of

Architecture his passion for studying historical architec-

ture and the proportions encoded within it. In my case,

this resulted in my doctoral thesis under the supervi-

sion of Professor Jacek Kościuk and Professor Mariusz

Ziółkowski. Without their support and assistance at every

stage of my research, it would have been impossible to

nd out whether the Incas used a standardised system of

measurements in the construction of royal buildings.

DOI: 10.37190/arc240104

Published in open access. CC BY NC ND license

Within the scope of the dissertation, a metrological

analysis of the interior layout of Inca buildings, i.e., the

niches and the spaces between them, was carried out us-

ing the cosine quantogram method, as well as an analysis

of the outlines and divisions of the fronts of the build-

ings, as a result of which the use of two modules was

observed: 42 cm and 54 cm. Even more interesting was

the variation in the use of modules in terms of the pur-

pose of the building: belonging to the Inca elite or their

servants [1].

The presented work is a study of the potential of sta-

tistical analysis of building outlines, for which we have

much less measurement data than the division of the

walls of the interior of the buildings and the measure-

ment of the structure is limited only to the contemporary

ground level. Therefore, metrological studies based on

the statistical method should be preceded by a techno-

logical analysis of the method of delineation of buildings

* ORCID: 0000-0001-5442-3947. Faculty of Architecture,

Wro cław University of Science and Technology, Poland, e-mail:

anna.kubicka-sowinska@pwr.edu.pl

Abstract

The metrological analysis of the Inca architectural elements at Machu Picchu using the cosine quantogram method was preceded by tests of

different models of building delineation and erection, which aim to test the method’s effectiveness in detecting the quantum with a differently defined

error occurring in the survey sample. The sources of such errors may lie in the work of Inca builders and the modern researcher. The measurements

of the architectural elements represent data from 3D laser scanning. The data obtained in this way refer to length measures that may have been

delineated using quantum: building outlines, dimensions and distribution of doorways, windows and niches. However, it is uncertain which of them

were actually planned by the Inca builders using the measure we are looking for (quantum) and which are incidental or outcome values.

Due to the sloping of the external walls towards the inside of the building, which was characteristic feature of Inca architecture, and the way in

which the buildings were planned (on horizontal terrain, sloping terrain or with projection onto the ground), the level at which the building is available

for measurement also has an important influence on the results of the analyses. This may be analogous to the level at which the building was planned,

or it may be significantly above that level. As a result of these factors, the group of tests concerns theoretically predictable combinations of the ways

in which the Inca buildings were delineated and the level available for measurement.

Tests of the effectiveness of the cosine quantogram method for Inca building outlines have shown that if they were laid out using some fixed

measure (quantum) then, regardless of how the building was delineated: levelled terrace, sloping ground, projection from level to sloping ground, the

cosine quantogram method must reveal its existence.

Key words: Peru, Inca architecture, building techniques, cosine quantogram, Cusco

1(77)/2024

Delineation of buildings at Machu Picchu by Inca builders 31

situated on articial terraces on the hillside. The system

of terraces and the resulting plazas required considerable

interference with the natural landscape and prior plan-

ning of the use of individual areas within a single estab-

lishment. The technology for constructing the terraces

required engineering and construction skills, but also hy-

draulic skills that had already been developed by earlier

Andean cultures. However, it was not until Inca times

that projects of this type began to be realised on such

a scale. The Cuzco region, and in particular the Urubam-

ba river valley, has the most elaborate architecture of this

kind. The Incan architecture built in this area was mainly

located on terraces, less frequently on levelled grounds.

The planning and layout of the rebuilding of the cap-

ital of the Inca Empire at Cuzco, including the layout

of the Temple of the Sun, was described in the mid-16

century by a Spanish chronicler [2]. The historical de-

scription of the transformation of the centre of power is

attributed to Pachakuti Inqa Yupanka, who was said to

have personally drawn the plans for the buildings and,

with the help of imperial ocials, supervised the con-

struction. According to the description, the ruler used

a measuring tool in the form of a rope (quechua: ñañu

waska [3]). Its length is not known from chronicle de-

scriptions, nor has material evidence of its existence

been found. However, it can be surmised that if such

a physical standard of measurement existed then its

length was a multiple of a basic modulus – the deriva-

tive of one of the anthropometric measures.

Proving the existence of a unit of measurement or

a system of measurement units that the Incas used

should therefore take place on the basis of a metrologi-

cal analysis of the constructions considered to be impe-

rial projects. In the cosine quantogram method chosen

for the purpose of such analysis, the existence of a spe-

cic unit of measure is not assumed, but it is veried

whether, in the selected series of measurements, we can

proof the existence of a basic unit of measure (mod-

ule) – the quantum [4]–[7]. For Inca architecture, the

cosine quantogram method has so far only been used

at the urban scale. It has proven itself as a method in

the analysis of cultivated terraces located in the Sacred

Valley (Yukay-Urubamba Valley). According to a study

by I. Farrington, the estimated quantum value for about

400 measurements is 1.615 m [8]. This corresponds to

the value of the rikra, an Incan measure known from

Spanish colonial-era chronicles and quechua dictionar-

ies. A multiplication of this value is the waska (4 times

the rikra), a measure used to measure greater distances

with a rope. Here, we can expect the use of both famil-

iar measures such as rikra and waska on the outlines of

buildings, but also smaller units mentioned in histori-

cal sources, such as: half of the fathom (sikya), khococ

(cubit), chaqui (foot) [9].

The architecture of the Machu Picchu site, the con-

struction of which is historically identied with Pacha-

kuti Inqa Yupanki, the same ruler who was said to have

used a rope to measure buildings in Cuzco, seems to be

appropriate research material for the search for a basic

unit of measurement used as an architectural module.

Unlike other examples equally representative of metro-

logical studies, such as the temple of the Sun in Cuzco

itself (which, however, was largely a subject of recon-

struction), Machu Picchu represents an architecturally

homogeneous complex, constrained by the local topog-

raphy. Here we nd clear traces of conscious planning

evident, for example, in the articial landscaping in the

form of terraces and levelled ceremonial plazas. The

extent of the reconstruction of the architectural relics

of Machu Picchu since its rediscovery by H. Bingham

is also known [10].

Due to the fragmentary nature of the archaeological

research of the foundation of buildings in the area, it is

not possible to determine whether the priority for mark-

ing out the foundations of buildings was to prepare the

terraces on which the foundation of the building was

then laid out, or whether the building was laid out on

an incline and the area around the building was later

levelled to the appropriate height [11].

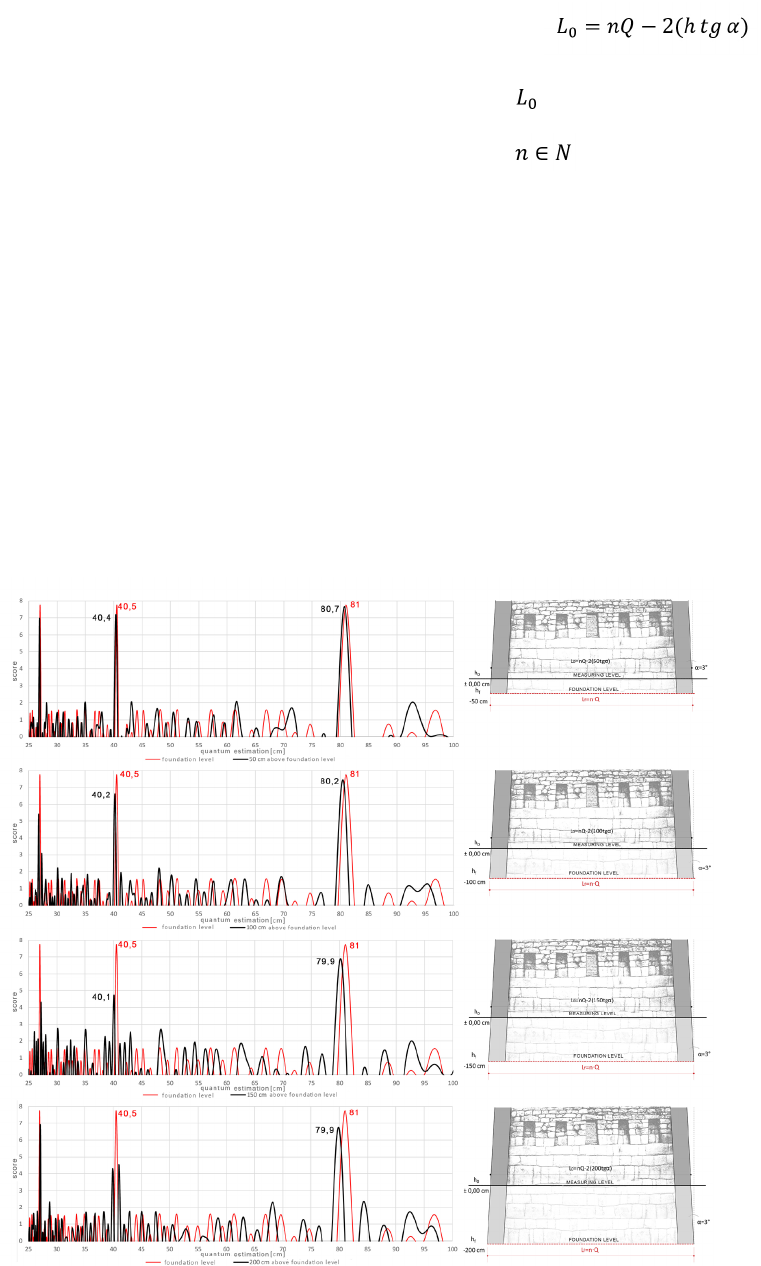
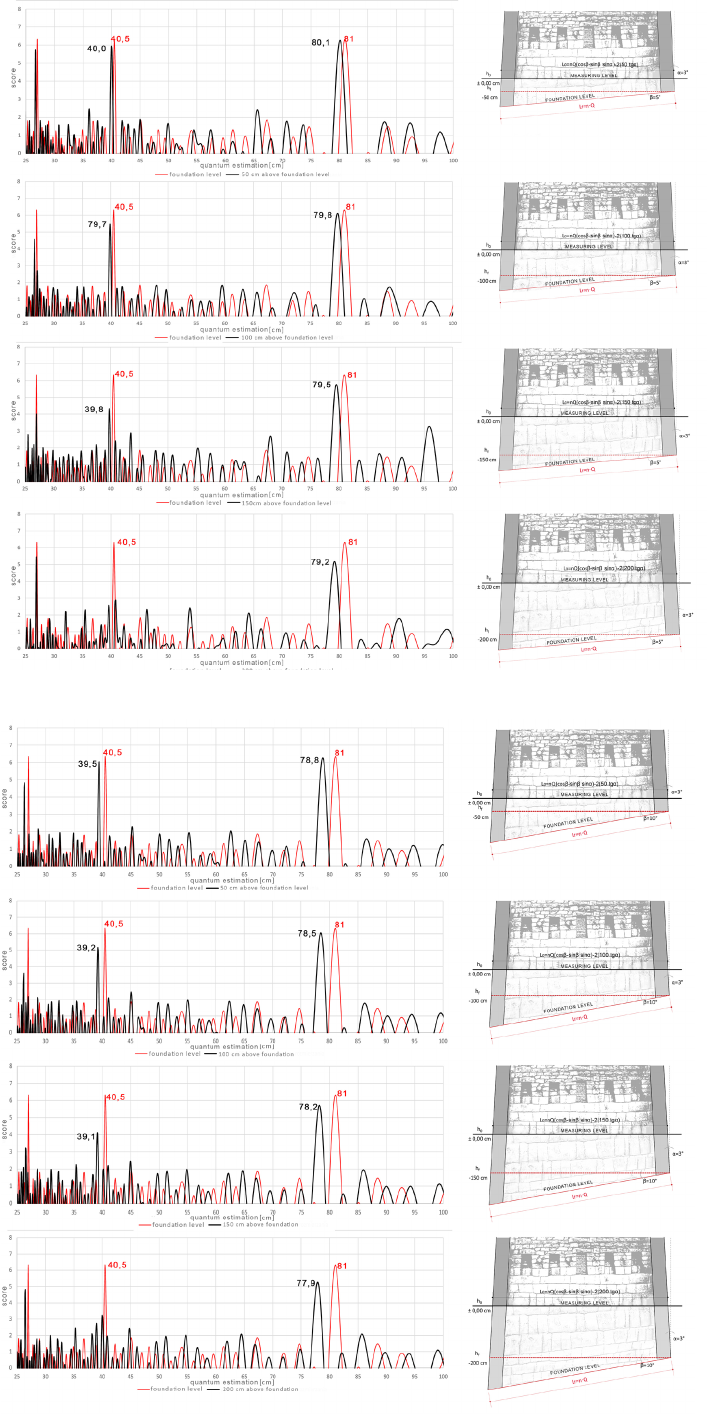
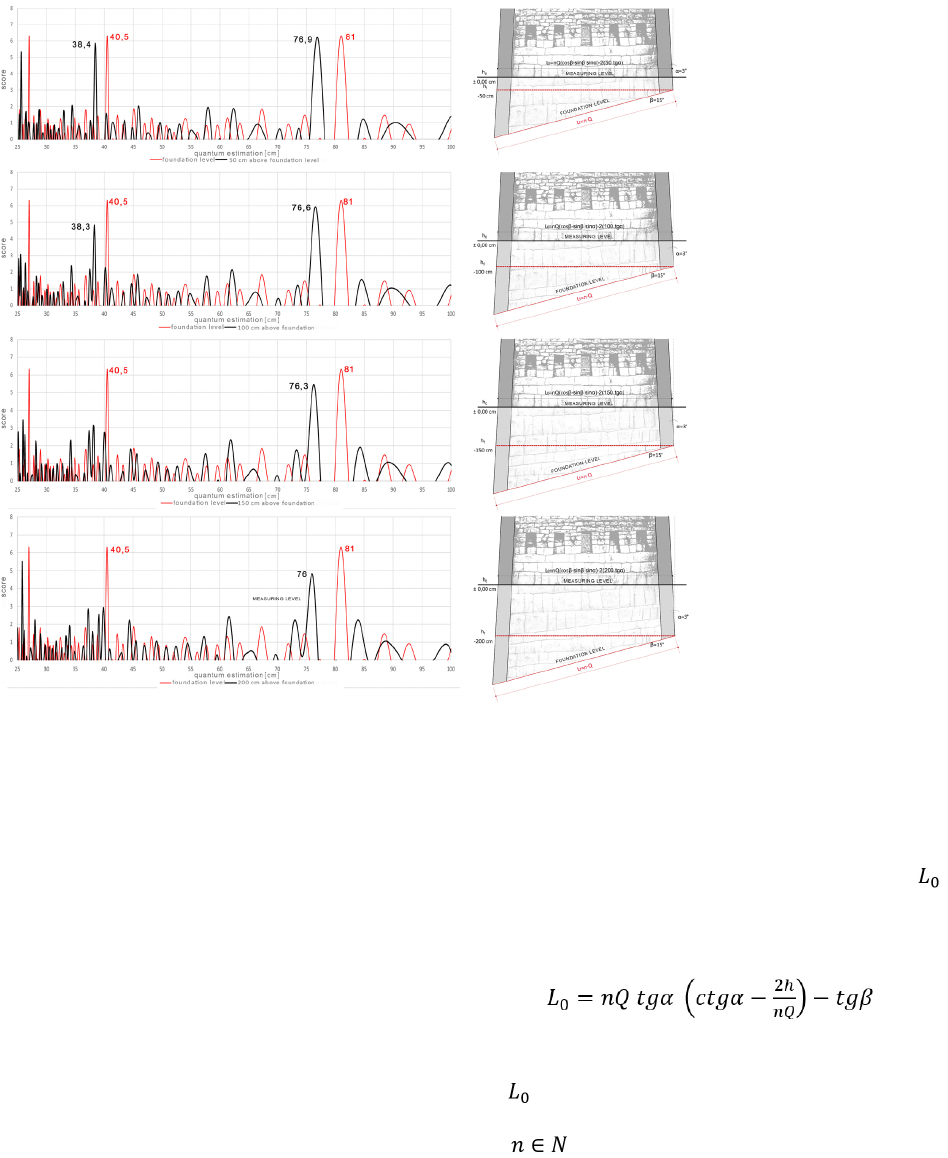
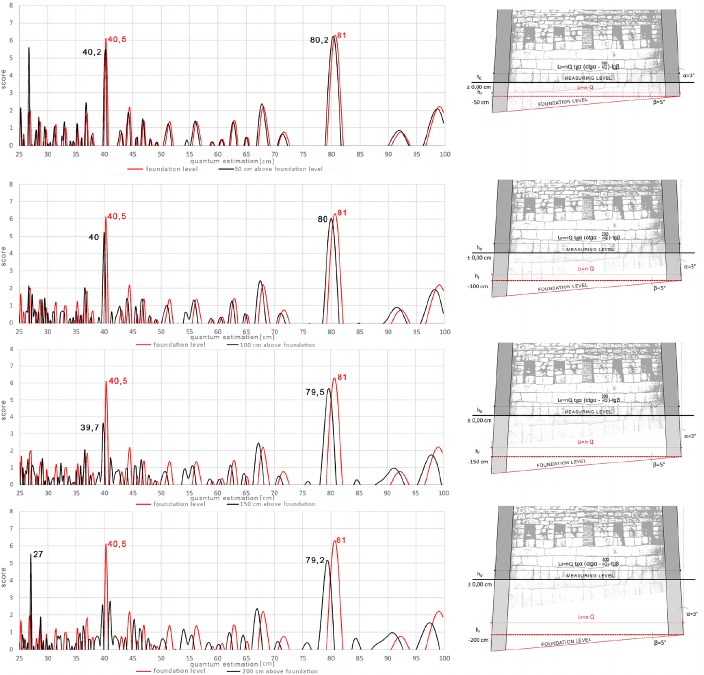
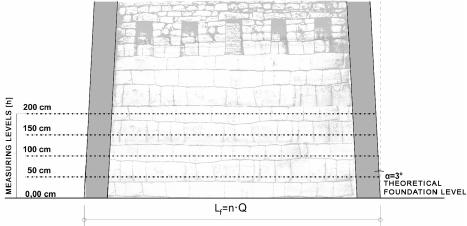
Testing quantum detection at different levels

available for measurement

Due to the non-invasive nature of the survey, archi-

tectural measurements from the 3D point cloud were

collected only above the current ground level, which in

only a few cases will correspond to the level at which

the building outline was measured by the former build-

ers. Due to the design of the walls, which are inclined

inwards at an angle of 3 to 6 degrees [12], [13], the re-

sults of the building outline measurements vary depend-

ing on the ground level available for measurement. The

quantum detection tests presented below are intended

to verify how dierent depths of the building arrange-

ment aects the value of the quantum estimation. The

basic assumption of this test is the existence of a level

or slope of the ground on which the building plans were

laid out according to a given unit of measurement.

Fig. 1. Schematic of quantum analysis for the different levels available

for measurement in relation to the theoretical foundation height on the

levelled terrain (elaborated by A. Kubicka-Sowińska)

Il. 1. Schemat analizy quantum dla różnych poziomów dostępnych

do pomiaru w stosunku do teoretycznej wysokości rozmierzania

obrysu na terenie zniwelowanym do poziomu

(oprac. A. Kubicka-Sowińska)

32 Anna Kubicka-Sowińska

Layout of building plans on levelled ground

From the randomly generated multiples of the quan-

tum situated at the layout level, the lengths of the building

outlines were calculated in proportion to the slope of the

walls and the height of the cut (Fig. 1). The trigonometric

functions for the angle α (1) were used:

(1)

where:

– length of building outline at measurement level h

Q – quantum 81 cm

α – wall angle

Fig. 2. Layout of building plans

on levelled ground (elaborated

by A. Kubicka-Sowińska)

Il. 2. Rozmierzanie planów

budynków na terenie

zniwelowanym do poziomu

(oprac. A. Kubicka-Sowińska)

The results of the quantum estimation (Fig. 2) are pre-

sented using randomly generated data (Table 1).

For this test model, a quantum of 81 cm is still detectable

even at a measuring level 200 cm away from the theoreti-

cal foundation level. The quantum value and its score varies

slightly from 79.9 cm (score: 6.80) to 81 cm (score: 7.8) as

the distance from the foundation level increases. The result of

the analysis shows that if there was a foundation level of the

Incan buildings on the at terrain then using the cosine quan-

togram method applied to the building outline data accessible

above foundation level will allow to nd the quantum. Its

value will be a deviation from the foundation level value, but

it will still be a representation of the maximum of the func-

tion and statistically it will not be a signicant dierence.

For the testing models of the buildings, the already

mentioned characteristic feature of Inca architecture

was taken into account: the slope of the walls, which for

the buildings of the Machu Picchu complex is between

3 and 4 degrees. Each of the tested models consists of

20 randomly generated dimensions, which are multiples

of the quantum, set as 81 cm (value of measure related

to sikya-half of a phanthom known as rikra). The theo-

retical foundation level in the models tested is no more

than 200 cm from the current ground level, the maxi-

mum value of which was determined on the basis of the

foundation part of the Incan buildings studied so far,

whose depth usually varies between 40 and 60 cm and

sometimes reaches more than 100 cm [14]. Furthermore,

the construction of the foundation walls was not made

by the Incan builders under such a steep slope as the

building walls and in some cases featured a foundation

oset. If all these variables were taken into account for

testing purposes, the number of combinations would in-

crease exponentially. For this reason, a simplied model

of the wall and foundation structure was adopted, taking

into account the variables α (wall angle), β (site angle),

h (foundation depth). The maximum value for the depth

of foundations adopted for testing will also compensate

for dierences when there are osets or a reduced an-

gle of inclination of the foundation walls. In order to

capture the variation in the estimated quantum value,

each building arrangement was carried out at depths of:

50 cm, 100 cm, 150 cm, 200 cm, assuming a wall incli-

nation of 3 degrees.

Delineation of buildings at Machu Picchu by Inca builders 33

No.

Multiplication Measurment of the building [cm]

1 12 972

2 13 1053

3 11 891

4 11 891

5 22 1782

6 7 567

7 20 1620

8 24 1944

9 24 1944

10 11 891

11 22 1782

12 12 972

13 19 1539

14 17 1377

15 5 405

16 13 1053

17 14 1134

18 9 729

19 15 1215

20 5 405

Table 1. Randomly generated data sample with a quantum multiple

of 81cm for the test: Layout of building plans on levelled ground

(elaborated by A. Kubicka-Sowińska)

Tabela 1. Losowo wygenerowana próba danych z wielokrotnością

quantum 81cm do testu: Rozmierzanie planów budynków na terenie

zniwelowanym do poziomu (oprac. A. Kubicka-Sowińska)

No. Multiplication Measurment of the building [cm]

23 1863

22 1782

23 1863

19 1539

18 1458

21 1701

13 1053

10 810

17 1377

8 648

11 891

16 1296

8 648

11 891

18 1458

13 1053

25 2025

23 1863

20 5 405

Table 2. Randomly generated data sample with a quantum multiple

of 81cm for the test: Delineating building plans on an inclined terrain:

5°, 10°, 15° (elaborated by A. Kubicka-Sowińska)

Tabela 2. Losowo wygenerowana próba danych z wielokrotnością

quantum 81cm do testu: Rozmierzanie planów budynków na skłonie

terenu: 5°, 10°, 15° (oprac. A. Kubicka-Sowińska)

Layout of building plans on an sloping terrain

Another model assumes that the outline of the build-

ing was delineated on an inclined terrain (5°, 10°, 15°)

(Fig. 3). This example was considered because of the ir-

regular prole of the bedrock on which the entire Machu

Picchu site was constructed. This also assumes that when

the contour of the foundations was laid out, the ground

was not levelled and the building was laid out on an in-

clination. This assumption can be justied by one of the

characteristics of the Incan stonework technique, in which

successive layers of stone blocks were adjusted to t ir-

regularities in the ground, such as outcrops of bedrock.

The largest stone blocks were treated in a similar way and

were left in their original position by adjusting successive

layers of construction to them.

Randomly generated quantum multiples at the foun-

dation level located on the sloping terrain were projected

onto a horizontal cutting plane corresponding to the the-

oretical measurement level. Given the angular dependen-

cies of the slope of the ground (β) and walls (α) and the

levels available for measurement, 50, 100, 150, 200 cm

below the foundation level. The building outline were cal-

culated according to the following equation: (2).

(2)

where:

– length of building outline at measurement level h

Q – quantum 81 cm

α – wall angle

β – the angle of inclination of the terrain on which the

building is placed

The results of the quantum estimation (Figs. 4-6) are

presented using randomly generated data (Table 2).

Fig. 3. Schematic of quantum analysis for the different levels available

for measurement in relation to the theoretical foundation height on the

inclination of the terrain (elaborated by A. Kubicka-Sowińska)

Il. 3. Schemat analizy quantum dla różnych poziomów dostępnych do

pomiaru w odniesieniu do teoretycznej wysokości fundamentu utworzonego

na nachyleniu terenu (oprac. A. Kubicka-Sowińska)

34 Anna Kubicka-Sowińska

Fig. 4. Delineating the building

plans on an inclined terrain of 5

degrees (elaborated by

A. Kubicka-Sowińska)

Il. 4. Rozmierzanie planów

budynku na skłonie terenu

równym 5 stopni (oprac.

A. Kubicka-Sowińska)

Fig. 5. Delineating the building

plans on an inclined terrain of

10 degrees (elaborated by

A. Kubicka-Sowińska)

Il. 5. Rozmierzanie planów

budynku na skłonie terenu równym

10 stopni (oprac. A. Kubicka-

Sowińska)

Delineation of buildings at Machu Picchu by Inca builders 35

Fig. 6. Delineating the building

plans on an inclined terrain of

15 degrees (elaborated by

A. Kubicka-Sowińska)

Il. 6. Rozmierzanie planów

budynku na skłonie terenu

równym 15 stopni (oprac.

A. Kubicka-Sowińska)

For randomly generated measurements with a multiple

of 81 cm, delineated on a slope of 5 degrees, quantum is

still detectable as a maximum function up to 200 cm below

the level available for measurement. Its value and score

change slightly: the value 80.1÷79.2 cm and the score

6.32÷5.17. Increasing the slope of the terrain to 10 degrees

has the expected eect of decreasing the calculated quan-

tum value 78.8÷77.9 cm in relation to the assumed 81 cm.

The score remains basically the same as in the previous

test. For a slope of 15 degrees, the calculated quantum val-

ue is even lower 76.9÷75 cm. At a distance of 200 cm,

from the foundation level, concurrent quantum values ap-

pear (25.8; 61.7; 73.1). Condence interval calculated for

the entire quantum estimate, reduce the reliability of the

obtained result. As in the previous tests taking into account

the error occurring in the measured quantum and here in

each quantum estimation variant the sub-values: 1/2; 1/3;

1/5 of the quantum, signicantly reduce their score.

Layout of building plans horizontally with projection

of multiples of quantum on the inclined terrain

Laying foundations on sloping ground can also imply

another method of delineation – the projection of horizon-

tally measured distances onto sloping terrain. This case

further increases the dierence between the dimensions

of the buildings at the level of foundation and the length

buildings collected at the level available for measurement.

The test was carried out for values of wall angle (α=3°)

and slope of the terrain (β=5°, 10°, 15°) (Fig. 7).

For randomly generated data containing multiples of

quantum 81 cm, the lengths of the building outlines ( )

were calculated taking into account the heights h of the

inclination angles α and β according to formula (3).

(3)

where:

– length of building outline at measurement level h

Q – quantum 81 cm

α – wall angle

β – the angle of inclination of the terrain on which the

building is placed

The results of the quantum estimation (Fig. 8) are present-

ed using randomly generated data (Table 3).

Despite the dierent way of delineation of the build-

ing, the results of the quantum estimation for a slope of

5 degrees, at dierent measurement levels are very

similar to the previous test. The value of the obtained

quantum with the increase of the depth changes from

36 Anna Kubicka-Sowińska

Fig. 7. Schematic of quantum analysis for different measuring

level with the foundation level delineated horizontally and then

projected the length on the slop of the terrain

(elaborated by A. Kubicka-Sowińska)

Il. 7. Schemat analizy quantum dla różnych poziomów pomiaru planu

budynku z uwzględnieniem rozmierzania quantum w poziomie

i odrzutowaniem odległości na skłon terenu

(oprac. A. Kubicka-Sowińska)

Table 3. Randomly generated data sample with a quantum multiple

of 81cm for the test: Horizontal building plan layout with projection

of multiples of quantum onto slope: 5°, 10°, 15° (elaborated by

A. Kubicka-Sowińska)

Tabela 3. Losowo wygenerowana próba danych z wielokrotnością

quantum 81cm do testu: Rozmierzanie planów budynków w poziomie

z odrzutowaniem wielokrotności quantum na skłon terenu: 5°, 10°, 15°

(oprac. A. Kubicka-Sowińska)

No. Multiplication Measurment of the building [cm]

1 19 1539

2 23 1863

3 17 1377,0

4 6 486

5 24 1944

6 24 1944

7 18 1458

8 25 2025

9 11 891

10 21 1701

11 7 567

12 20 1620

13 23 1863

14 20 1620

15 16 1296

16 25 2025

17 12 972

18 21 1701

19 19 1539

20 23 1863

a table (Table 4). Similarly to the previous test, the val-

ue of the quantum obtained changes with increasing

slope and reaches similar values.

Summary of tests of the effectiveness of the cosine

quantogram method in detecting quantum

in the outlines of Inca buildings

Tests of the eectiveness of the cosine quantogram

method for the outlines of Incan buildings have shown

that if they were delineated using some xed unit of

measurement (quantum) then, regardless of the way

in which the building was delineated (levelled ter-

race level, slope of the terrain, projection from level

to slope of the terrain), the cosine quantogram meth-

od must reveal its existence. Based on the assumption

that the building outlines were laid out using the ba-

sic unit of measurement, we can prove its existence

up to a distance of 200 cm between the hypothetical

foundation level and the level available for measure-

ment. In the tests presented above, the sloping wall

construction and the slopes of the terrain obviously

aected the value of the quantum itself. In the most

extreme case, the dierence in quantum value was

5 cm. This leads to the conclusion that in the case of long

dimensions with numerous multiples of the quantum

(e.g., building outlines), we are not able to determine un-

ambiguously what the exact value of the standard measure

was, but we can certainly prove its existence. Quantum

analysis of buildings outline which were laid out using

a module will appear in the function graph as a max-

imum point but its value could be interrupted by the

distance to original foundation level.

The observations from this experiment were taken into

account during the metrological analysis of the building

outlines at Machu Picchu. Wide range of bootstrap con-

dence intervals calculated for the quantum results shows

Table 4. Results for the test: Horizontal building plan layout with

projecting multiples of quantum per slope: 10°, 15°

(generated by A. Kubicka-Sowińska)

Tabela 4. Wyniki dla testu: Rozmierzanie planów budynków

w poziomie z odrzutowaniem wielokrotności quantum na skłon

terenu: 10°, 15° (oprac. A. Kubicka-Sowińska)

Inclination of

the terrain

Measuring

level [cm]

Maxima of the function

(quantum) [cm]

and score

10°

50 79,9 ; 6,2

100 79,5 ; 6

150 79,1 ; 5,6

200 26,9 ; 5,39

15°

50 79,5 ; 6,4

100 79,1 ; 6,1

150 78,8 ; 5,6

200 78,4 ; 5

80.2÷79.2 cm in relation to the assumed 81 cm, and its

score decreases from 6.2÷5.2. Due to the similarity of

the results, the graphical representation of the result of

this test has been limited only to the ground inclination

angle β= 5°, and the remaining results for the angle

β= 10° and β= 15° have been presented in the form of

Delineation of buildings at Machu Picchu by Inca builders 37

Fig. 8. Delineation building plans

horizontally with a projection of

multiples of quantum on a slope of

5 degrees (generated by

A. Kubicka-Sowińska)

Il. 8. Rozmierzanie planów

budynków w poziomie

z odrzutowaniem wielokrotności

quantum na skłon terenu równy

5 stopni (oprac. A. Kubicka-

Sowińska)

that in the outlines of Machu Picchu houses there is no de-

lineation using quantum (module). At least there is no sta-

tistical evidence of using a quantum in building outlines

by ancient construction workers. A negative result from

the use of the module may be due to both too few meas-

urements (less than 20) and the inclusion in the measure-

ment sample of a large number of dimensions that were

not measured using the module, but are, for example, the

result of the available tract depth (depth of terrace). For

example, only one wall – the front one – could be de-

termined in the building outline, while the length of the

others was a result of the size of the available terrain. It

should be noted, however, that with the terrain being so

dicult to manage, most of the main dimensions of the

building were rather dictated by the topography of the site.

Acknowledgments

Thanks to the cooperation with the Centre for Pre-Co-

lumbian Studies of the University of Warsaw (OBP) and the

Centre for Andean Studies of the University of Warsaw in

Cusco (CEAC) led by Professor Mariusz Ziółkowski, the

Author had the opportunity to conduct eld research at Ma-

chu Picchu. This happened thanks to a cooperation agree-

ment between CEAC and the Directorate of the Machu Pic-

chu National Archaeological Park, initiated already in 2007

with a joint Polish-Peruvian research project. The accession

to this agreement as a partner of the 3D Scanning and Mod-

elling Laboratory of the Wrocław University of Science and

Technology, led by Professor Jacek Kościuk, PhD, architect,

made it possible to collect and use measurement data from

terrestrial 3D laser scanning of the Machu Picchu site.

38 Anna Kubicka-Sowińska

Streszczenie

Wytyczanie budynków w Machu Picchu przez inkaskich budowniczych

– czy analiza metrologiczna obrysów budynków jest możliwa bez inwazyjnych badań?

Analizę metrologiczną elementów architektury inkaskiej na Machu Picchu przy użyciu metody cosine quantogram poprzedziły testy różnych

modeli wytyczania i wznoszenia budynku, które mają na celu sprawdzenie skuteczności metody w wykrywaniu quantum przy różnie zdefiniowanym

błędzie występującym w badanej próbie pomiarowej. Źródła takich błędów mogą leżeć zarówno po stronie inkaskich budowniczych, jak

i współczesnego badacza. Pomiary elementów architektury stanowią dane zebrane podczas laserowego skanowania 3D. Dane pozyskane w ten

sposób odnoszą się do miar długości, które mogły być rozmierzane z użyciem quantum: obrysów budynków, wymiarów pomieszczeń, wymiarów

i rozmieszczenia otworów drzwiowych, okiennych i nisz. Nie ma jednak pewności, które z nich były faktycznie rozmierzane przez inkaskich

budowniczych z użyciem poszukiwanej przez nas miary (quantum), a które są wartościami przypadkowymi lub wynikowymi.

Ze względu na charakterystyczne dla architektury inkaskiej pochylenie ścian zewnętrznych do wnętrza budynku oraz nierozpoznany do tej pory

sposób rozmierzania budynków (na poziomym terenie, skłonie terenu lub z odrzutowaniem na teren), istotny wpływ na wyniki analiz ma też poziom,

na którym budynek jest dostępny do pomiaru. Może on być analogiczny do poziomu, na którym rozmierzano budynek lub też być położony znacznie

powyżej tego poziomu. W związku z tymi czynnikami poniższa grupa testów dotyczy dających się teoretycznie przewidzieć kombinacji sposobów

rozmierzania budynków inkaskich i poziomu dostępnego do pomiaru.

Testy skuteczności metody cosine quantogram dla obrysów budynków inkaskich wykazały, że jeśli były one rozmierzane z użyciem jakiejś stałej

miary (quantum) to niezależnie od sposobu wytyczania budynku (zniwelowany poziom tarasu, skłon terenu, odrzutowanie z poziomu na skłon

terenu) to metoda cosine quantogram musi ujawnić jej istnienie.

Słowa kluczowe: Peru, architektura inkaska, techniki budowy, cosine quantogram, Cuzco

[1] Kubicka-Sowińska A., Sieczkowska D., Bastante J., Inca builders

at Machu Picchu National Archaeological Park, “Archaeometry”

2023, 4(66), 1–15, https://doi.org/10.1111/arcm.12849

[2] Betánzos J. de, Suma y Narracion de los Incas, M. del Carmen Mar-

tín Rubio (ed.), Ediciones Atlas, Madrid 2004 (1551).

[3] Holguín D.de González, Vocabulario de la lengua general

de todo el Peru, Lima 1608, https://archive.org/details/

vocabulariodelal01gonz/page/n3, 206 [Accessed: 08.11.2017].

[4] Pakkanen J., Deriving ancient foot units from building dimensions:

A statistical approach employing cosine quantogram analysis,

[in:] G. Burenhult, J. Arvidsson (ed.), Archaeological informatics:

Pushing the envelope – CAA 2001 – Computer applications and

quantitative methods in archaeology. Proceedings of the 29

con-

ference, 501–506.

[5] Pakkanen J., The Temple of Athena Alea at Tegea: Revisiting de-

sign-unit derivation from building measurements, [in:] E. Ostby

(ed.), Third international seminar on ancient arcadia, Held at the

Norwegian Institute at Athens, Ateny 2002, 167–183.

[6] Pakkanen J., The Temple of Zeus at Stratos: New observations on the buil-

ding design, “Arctos – Acta Philologica Fennica” 2004, 38, 95–121.

[7] Pakkanen J., The Toumba building at Lefkandi: A statistical method

for detecting a design-unit, “The Annual of the British School at

Athens” 2000, 99, 257–271.

[8] Farrington I., Medidas de tierra en el Valle de Yucay, Cusco, “Gaceta

Arqueológica Andina” 1984, 11, 10–11.

[9] Rowe J.H., Inca culture at the time of the Spanish conquest, [in:]

J. Steward (ed.), Handbook of South American Indians, Vol. 2,

Washington 1946.

[10] Machupicchu 100 años después, Ministerio de Cultura Dirección

Desconcentrada de Cusco, Cuzco 2014.

[11] Hyslop J., Inca settlement planning, University of Texas Press,

Austin 1990.

[12] Farrington I., Cusco: Urbanism and Archaeology in the Inka

World, University Press of Florida, Gainesville 2013.

[13] Protzen J.P., Inca architecture, [in:] L. Laurencich-Minelli (ed.), The

Inca World: The Development of Pre-Columbian Peru, AD 1000–

1534, University of Oklahoma Press, Norman 2000, 193–216.

[14] Protzen J.P., Inca Architecture and Construction at Ollantaytambo,

Oxford University Press, Oxford 1993.

References