“Nodes and Spatial Structures”, a tribute to Stéphane du Château

René Motro

doi:10.5277/arc140404

Abstract

The work of Stéphane du Château is clearly inscribed in the second half of the 20th century. He developed several spatial structures’ systems based on a clever design of nodes, which were all patented. More than two hundred and fifty projects were effectively built. Besides this productive work Stéphane du Château founded several associations in order to gather designers and to promote Spatial Structures. His charisma and his commitment were the keys of a remarkable contribution to spatial structures. This paper is a short summary and a reminder of his achievements and importance for the development of spatial structures.

Full article view is only available on bigger screens.

2014

4(40)

DOI: 10.5277/arc140404

René Motro*

„Węzły i struktury przestrzenne” – w hołdzie Stefanowi du Château

“Nodes and Spatial Structures”, a tribute to Stéphane du Château

Wprowadzenie

Stefan du Château urodził się w Solwyczegodzku

w 1908 r., a po drugiej wojnie światowej, aż do swojej

śmierci w 1999 r., pracował we Francji.

Nie mam żadnych wątpliwości co do tego, że to on wła-

śnie wprowadził mnie w świat struktur przestrzennych,

znając moje zainteresowanie tym tematem. O ile dobrze

pamiętam, pierwszy raz spotkaliśmy się w Szkole Archi-

tektury w Montpellier, gdzie uczyłem wytrzy małości ma -

teriałów. Trzy lata wcześniej, w roku 1966, uczestniczył

w bardzo interesującej, pierwszej Międzynarodowej Kon-

ferencji nt. Struktur Przestrzennych w Guild fordzie, zor-

ganizowanej przez Zygmunta Stanisława Makowskiego

(il. 1). Stefan du Château był jednym z au torów uczest-

niczących w tym wydarzeniu; jego praca zatytułowana

była L’intégration de la pensée technique dans la création

architecturale. Została ona ujęta w części 7.: „Projekt:

Przyszłość” [1]. Tytuł mówi wszystko. „Myśl technicz-

na”, „tworzenie”, „architektura” – te słowa dobrze opisują

tego człowieka. Praca był

a napisana po francusku (auto-

rzy tacy jak M. Mengeringhausen i Y. Friedman również

pisali artykuły konferencyjne w swoich języ kach ojczy-

stych), ale Stefan du Château zawsze mówił po francusku

i od czasu do czasu w latach następnych prosił mnie o tłu-

maczenie swoich wykładów.

W tamtych latach, tworzący jednocześnie wybitni pro -

jektanci, tacy jak Frei Otto i Eduardo Torroja, mogli pre -

* Uniwersytet w Montpellier, Francja/University Montpellier 2,

Montpellier, France.

Introduction

Stéphane du Château, was born in Solvychegodsk, in

1908, and after the second world war, worked in France,

until his death in 1999.

He clearly introduced me in the world of spatial struc-

tures, knowing my personal interest for this ﬁ eld. As far

as I remember we met for the ﬁ rst time in Mont pellier

at the School of Architecture where I taught strength of

ma terials. Three years before, in 1966, he attended the ﬁ rst

International Conference on Space Structures in Guildford,

this conference was organized by Zyg munt Stanis ław Ma-

kowski. The proceedings were very impressive (Fig. 1).

Du Château was one of the authors who participated to

this event, his paper was titled L’intégration de la pensée

technique dans la création architecturale. It was includ-

ed in the part 7 “Design: The Future” [1]. Every thing is

said in this title. “Technical thought”, “creation”, “archi-

tecture” these words described the man. The paper was

written in French (and authors like M. Mengeringhausen

and Y. Friedman wrote in conference proceedings also

in their own native language), but Stéphane du Château

always spoke French, and from time to time, du ring

the following years he asked me to translate his lectures.

It was in these years when simultaneously eminent

designers, Frei Otto, Eduardo Torroja were able to sub-

mit innovative lightweight structures taking advantage of

emerging numerical methods. In 1962 Nicolas Esquillan,

the designer of the CNIT (Paris), organized the IASS

Symposium in the capital of France. This event was de-

International Association for Shell and Spatial Structures.

42 René Motro

zentować swoje innowacyjne i lekkie struktury, korzys ta jąc

z możliwości, które dawały nowe metody nu me rycz-

ne. W roku 1962 Nicolas Esquillan, projektant zwią zany

z CNIT w Paryżu, zorganizował w stolicy Francji sympo-

zjum International Association for Shell and Spa tial Struc -

tures (IASS)

. Wydarzenie to było poświęcone „wiszącym

dachom” i Frei Otto wygłosił swój pierwszy wykład pod

tytułem „Einleitende Bemerkungen zum Kolloquium”.

International Association for Shell and Spatial Struc-

tures zostało założone trzy lata wcześniej przez Eduarda

Torroję. Du Château namawiał mnie, żebym wstąpił do

tego Stowarzyszenia. I tak też zrobiłem.

Wybitna osoba

Z pewnością niewielu ludzi miało możliwość zoba-

czyć go na konferencjach bez słynnej muszki, symbolu

wytworności i szczerej uprzejmości. Była ona sym bolem

jego głębokiego człowieczeństwa i kultury. Jako architekt

z wykształcenia, zawsze głosił potrzebę dobrego zro-

zumienia istoty sprawy. Przywiązany był bardzo do języ-

ka francuskiego i uważał to za punkt honoru, aby za bierać

głos w tym języku, upewniając się najpierw, że większość

uczestników będzie mogła go zrozumieć. Prezentując

swoje prace, zawsze korzystał ze slajdów, których całą

kolekcję otrzymał później Uniwersytet w Mont pellier

dzię ki mieszkającemu na południu Francji siostrzeńco-

wi Stefana. Architekt, inżynier, ale także malarz Stefan

du Château był kimś, kogo określa się po francusku un

honnête homme. Jego prace i życiorys dobrze opisał Tade-

usz Barucki [2]. Nie trzeba przy tym dodawać, że biuro du

Château w Paryżu było miejscem, gdzie jego rodacy za-

wsze mogli uzyskać pomoc i opiekę, której potrzebowali.

Międzynarodowe Stowarzyszenie Konstrukcji Powłokowych

i Prze strzennych.

voted to “Hanging Roofs” and Frei Otto gave his ﬁ rst lec-

ture titled “Einleitende Bemerkungen zum Kolloquium”.

The International Association for Shell and Spatial

Structures was founded three years earlier by Eduardo

Torroja. Stéphane du Château urged me to join this Asso-

ciation, I did.

A distinguished person

Certainly few people saw him in conferences with-

out his famous bow tie, symbol of distinction and sin-

cere courtesy. This was the symbol of his deep human-

ity and culture. Educated as architect he always claimed

the necessity to have a good understanding of the essen-

ce of the program. Attached to the French language,

he made it a point of ho nor to make interventions in

French, having made sure that a majority of the attend-

ing persons could understand him. He always presented

his works with slides, and actually University of Mont-

pellier received the whole collection of them, thanks to his

nephew; lives in the south of France. Architect, engineer

but also painter Stéphane du Château was in the French

meaning un honnête homme. His works and curricu lum

are well described by Tadeusz Barucki [2]. Is it not ne-

cessary to say, that his ofﬁ ce in Paris was the place where

his fellow countrymen were insured to ﬁ nd the assistance

and the welcome which they needed.

An imaginative engineer

Basic ideas

Stéphane du Château was one of the most productive

engineers in the ﬁ eld of spatial structures during the se-

cond half of the 20

century. He was a specia list of tubular

construction and worked in close relation with Zygmunt

Stanisław Makowski who was established in London

Il. 1. Stefan du Château (a),

okładka Proceedings of the 1

International Conference on

Space Structures (b)

(fot. R. Motro)

Fig. 1. Stéphane du Château (a),

cover of Proceedings of the 1

International Conference on

Space Structures (b)

(photo by R. Motro)

„Węzły i struktury przestrzenne” – w hołdzie Stefanowi du Château / “Nodes and Spatial Structures”, a tribute to Stéphane du Château 43

Inżynier z wyobraźnią

Podstawowe idee

Stefan du Château był jednym z najbardziej produk-

tywnych inżynierów w dziedzinie struktur przestrzen-

nych 2. poł. XX w. Był specjalistą od wykorzystania rur

do budowy konstrukcji i blisko współpracował z Zyg-

muntem Sta nisławem Makowskim, który działał w Lon-

dynie (w Imperial College), a później także w Guild-

fordzie (w Space Structure Research Centre

). Różnica

po między słowami „przestrzeń” a „przestrzenny” nie ma

znaczenia w niniejszym tekście

. Stefan du Château był

specja listą w dziedzinie geometrii i potraﬁ ł projekto wać

wszelkiego rodzaju struktury przestrzenne: ruszty dwu-

war stwowe, sklepienia, systemy podwójnie zakrzywio-

ne..., ale zawsze szczególnie interesowały go dwa zagad-

nienia: węzły oraz proces uprzemysłowienia. Każdy, kto

zajmował się strukturami przestrzennymi, wie, że kluczo-

wym zagadnieniem do rozwiązania w tym zakresie jest

projekt węzłów.

Węzły

• Rozwiązanie dwukierunkowe – Unibat

Na początku rozwoju badań nad rusztami dwuwars t-

wo wymi większość z nich była dwukierunkowa. Miały

one dwie równoległe warstwy – „górną” i „dolną” – z ele-

mentami wiążącymi pomiędzy nimi. Z geometrycznego

punktu widzenia jednym z rozwiązań było uzyskanie

względnego obrotu o 45° pomiędzy głównymi kierunka-

mi warstwy górnej i warstwy dolnej, z których każda była

kwadratową siatką. Stefan du Château był przekonany, że

to bardziej efektywne niż rozwiązanie „kwadrat na kwa-

dracie”. Potwierdzają to wyniki, które opublikowałem

w 1975 r. [3]; ciężar własny został znacznie zmniejszony.

Jestem wdzięczny Stefanowi du Château, Zygmuntowi

Stanisławowi Makowskiemu i Hoshyarowi Nooshinowi,

którzy zachęcili mnie do wykonania tej pracy podczas

mojej wizyty w Centrum Badań Struktur Przestrzennych

w Guildfordzie (1973).

Co było węzłem w takiej geometrii, w systemie Unibat?

Nic, ponieważ nie ma żadnych części węzłowych w tej

sieci dwuwarstwowej. Jest to stosowane w pira midach

o podstawie kwadratowej, montowanych przy użyciu jed-

nej poziomej śruby na rogach kwadratów, które stano wią

warstwę górną (podstawę piramid). Pozostałe krawędzie

piramidy są elementami usztywniającymi. Warstwa dolna

jest najprostsza: elementy nie są docinane do wymiarów

geometrycznych, całkowita długość rur jest zachowana,

ale są one zgniatane w odpowiednich odległościach i prze-

wiercane tak, aby wprowadzić w nie śrubę przechodzącą

przez dwa elementy warstwy dolnej krzyżujące się pod

Centrum Badań Struktur Przestrzennych.

W języku angielskim konstrukcje przestrzenne określa się termi-

nem „spatial structures”. Jednak Z.S. Makowski używał także określenia

„space structures” i założony przez niego ośrodek badawczy nazywa się

Space Structures Research Centre. Ten drugi termin jest obecnie

używany przede wszystkim w kontekście prac tego ośrodka.

(at Imperial College), and then in Guildford, Surrey (at

the Space Structure Research Centre). The difference be-

tween the two words “space” and “spatial” is meaning-

less in this paper. Stéphane du Château was a specialist

of geometry and was able do design all kinds of spatial

structures: double layer grids, vaults, double curved

systems... However, he was always concerned with two

problems: the node and the industrialization process. All

people who were involved in spatial structures design,

know that the main question to solve is the node design.

Nodes

• Bidirectional solutio n – Unibat

At the beginning of investigations into double-layer

grids, most of them were bidirectional. They contained

two parallel layers, “top” and “bottom” ones, and in be-

tween bracing members. Geometrically speaking one of

the solutions was to get a forty ﬁ ve degrees relative ro-

tation between the main directions of the top layer and

the bottom layer, both being a square meshing. Stéphane

du Château was convinced that it was more efﬁ cient than

a “square on square” choice. This was conﬁ rmed by the

results that I published in 1975 [3]; self-weight was sig-

niﬁ cantly reduced. I am indebted to Stéphane du Château,

Zygmunt Stanisław Makowski and Hoshyar Nooshin who

urged me to do this work, when I visited the Space Struc-

tures Centre in Guildford (1973).

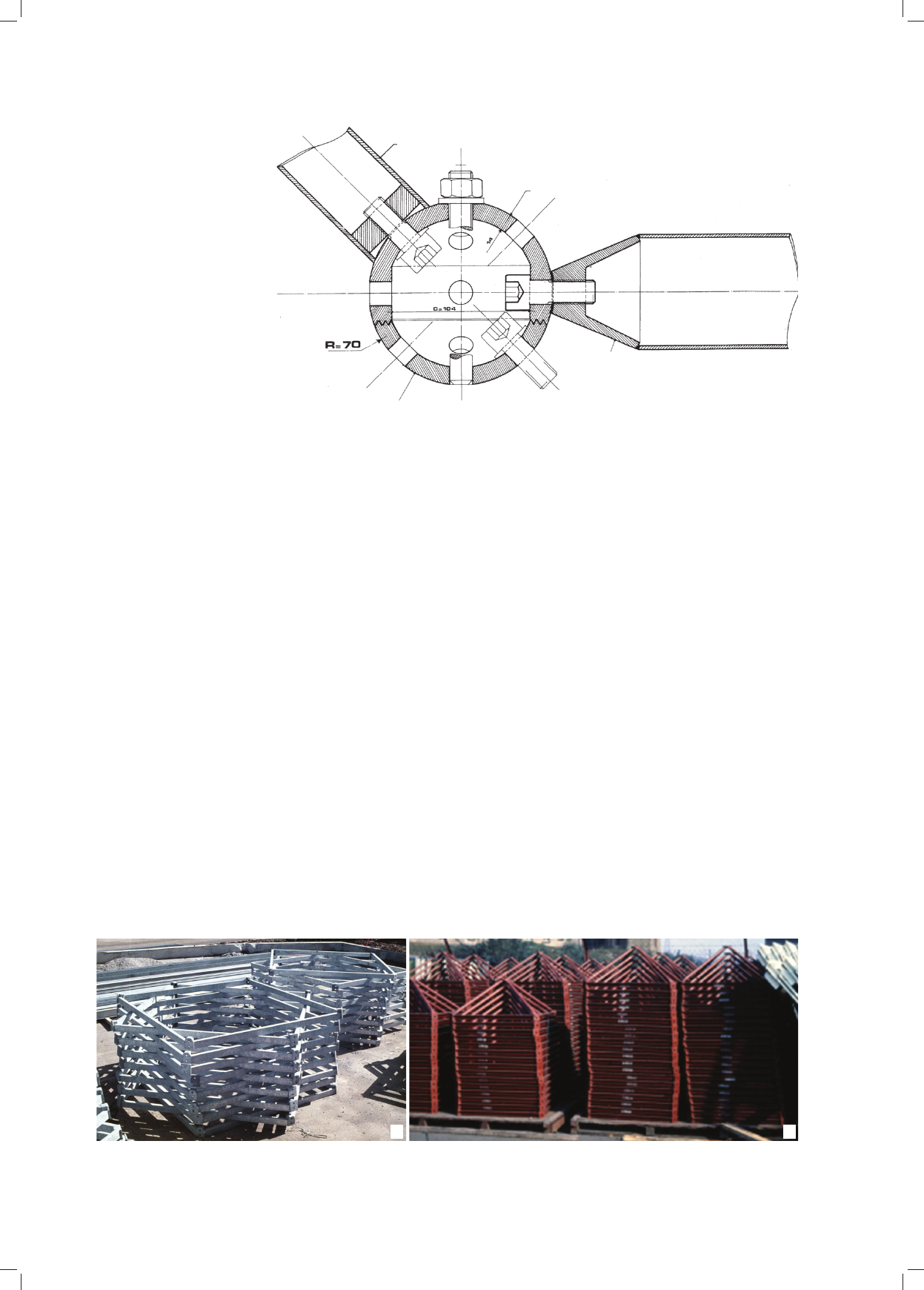
Which was the node for this geometry, for this Unibat

system? None, since there are no node parts for this dou-

ble layer grid. It is realized with square pyramids that are

assembled by a single horizontal bolt at the corners of

the squares that constitute the upper layer (basis of the

pyramids). The other edges of the pyramid are the brac-

ing members. The bottom layer is the simplest that can be

found: members are not cut to meet the geometrical sizes,

the whole length of tubes is kept, but they are crushed at

ne cessary distances and drilled so as to introduce a bolt

through two bottom layer members crossing at 90°, and the

apex of the pyramid where four bracing members are joined.

It can be said that this is a solution without nodes, or with

bolts as nodes: the simplest solution that could be found.

Lightness and transparency result from this design.

In 1976, I organized a colloquium on structures in Mont-

pellier [4], and for this event we assembled two double

layer grids so as to constitute a kind of vault inside our

University (Fig. 2).

• Three directional solutions

Stéphane du Château was also aware of the structural

efﬁ ciency of the double curved system and realized what

he called a “three directional” cupola in Grandval with

a very clever molded steel node. This cupola has a dia-

meter equal to 42 m. The radius of the complete sphere

is equal to 40 m. With a sag of 6 m, the total length of

members is 2,136 m, and there are 313 nodes.

Stéphane du Château was convinced by the rigidifying

effect of the double positive curvature, and simultane-

ously by the efﬁ ciency of the three-directional orienta-

tion of the members that was also in accordance with the

44 René Motro

kątem 90° oraz na wierzchołku piramidy, gdzie połączone

są cztery elementy wiążące. Można powiedzieć, że jest

to rozwiązanie bez węzłów lub ze śrubami stanowiącymi

węzły; najprostsze możliwe rozwiązanie.

Taki projekt daje lekkość i przejrzystość. W roku 1976

zorganizowałem w Montpellier kolokwium na temat

struk tur [4] i na to wydarzenie zmontowaliśmy dwa ruszty

dwuwarstwowe, które tworzyły rodzaj sklepienia na tere-

nie naszego Uniwersytetu (il. 2).

• Rozwiązania trójkierunkowe

Stefan du Château zdawał sobie sprawę ze struktu-

ralnej efektywności zastosowania systemu podwójnie

zakrzywionego i w Grandval zrealizował coś, co nazwał

kopułą „trójkierunkową” z bardzo pomysłowo ufor mo-

wa nym stalowym węzłem. Ta kopuła ma średnicę 42 m.

Promień całej kuli sięga 40 m. Przy strzałce 6 m, łączna

długość elementów to 2136 m, a węzłów jest 313.

Du Château był przekonany o usztywniającym dzia -

ła niu podwójnej krzywizny dodatniej oraz jednocześ nie

o efektywności trójkierunkowej orientacji elementów, któ-

ra dodatkowo była zgodna z trójkątnym rzutem obiektu.

Problemem, który musiał rozwiązać, była siatka o po-

wierzchni podwójnie zakrzywionej. Warto podkreślić, że

z geometrycz nego pun

ktu widzenia nie jest łatwo ustalić

długość każdego elementu. Nawet jeśli trójkąty wygląda-

ją podobnie, w rze czywistości takie nie są, a w tamtych

czasach nie było odpowiedniego oprogramowania wspo-

magającego projektanta. Ale zasada opiera się na trzech

krzyżujących się ze sobą sześciokątnych regularnych łu-

kach oraz trójkątnym oddzieleniu pomiędzy nimi.

Projektanci radzili sobie z tym wyzwaniem, budując mo-

dele ﬁ zyczne w małej skali oraz mierząc długość każdego

elementu takiego modelu. Nie było to jednak zbyt precyzyj-

ne, a jednym z ograniczeń projektowania węzłów była moż-

liwość zmiany długości poszczególnych elementów pod-

czas samej realizacji. Konieczne było również znalezienie

sposobu na uzyskanie systemu po dwójnej krzywizny. Ste-

fan du Château zaprojektował i opatentował „węzeł SDC”.

System SDC rozwiązuje trzy główne problemy w taki

sposób, że:

– do każdego węzła może dochodzić sześć elementów;

–

dołączając odpowiednią liczbę rur wewnątrz węz-

ła, pro blem ograniczenia długości zostaje rozwiązany.

Wszys t kie elementy mogą mieć ten sam rozmiar, różnice

są niwe lo wane poprzez zmianę długości poprzez wsunię-

cie do węzła;

– krzywizna jest możliwa, ponieważ przestrzeń we-

wnątrz węzła umożliwia zapewnienie wymaganego na-

chylenia elementów (wystarczy zaledwie kilka stopni).

Po uzyskaniu przez projekt odpowiedniej geometrii,

następnym krokiem jest wybór sposobu realizacji. Głów-

nym sposobem realizacji jest spawanie: węzeł składa się

z dwóch części zespawanych ze sobą przy prawidłowym

ułożeniu elementów spełniającym ograniczenia geome-

tryczne wymiarów i kątów. Mniejsze grupy elementów są

łączone na ziemi, a następnie włączane do całej struktu-

ry przestrzennej.

Jeśli chodzi o płaskie podwójne sieci trójkierunko-

we, warto może również opisać inne rozwiązanie za-

triangular in plane shape. He had to solve the meshing

of the double curved surface. It is worth saying that geo-

metrically speaking it is not easy to determine the length

of every member. Even if triangles look similar they are

not, and in those times there was no form-ﬁ nding soft-

ware to help the designer. But the principle relies on three

intersecting hexagonal regular arches, and in between

a triangular partition.

But designers used to build physical models in small-

scale and to measure the length of every member of this

model. The precision was not achieved exactly, and one

of the constraints for the node design was to allow length

modiﬁ cation during the realization itself. It was also ne-

cessary to ﬁ nd a way to get a double curvature system. Sté -

phane du Château designed and patented the “SDC node”.

The three main problems are solved in SDC system in

such a way that:

– every node can receive six members;

– by adding an appropriate number of tubes inside the

node, the length constraint is solved. All members can be

of the same size, the variations are absorbed by the pen-

etration length inside the node;

– the curvature is possible since the space inside the

node allows providing the required inclination of the

members (only some degrees are sufﬁ cient).

Once the design has achieved proper geometry, the fol-

lowing step is to choose a realization process. Welding is the

main method go verning this process: the node is molded in

two parts that are welded together when members are cor-

rectly in place meeting the geometrical constraints of size

and angles. Subgroups of members are realized at ground

level and then included in the whole spatial structure.

As far as three directional ﬂ at double grids are con-

cerned, it can be also useful to describe another solution

double layer, built in Nîmes, close to the highway.

The design principle chosen by Stéphane du Château is

similar to bidirectional solutions presented above: tubes

are crushed and drilled (bottom layers), and in this case

speciﬁ c pieces are designed for joining members of the

Il. 2. Dwa ruszty dwuwarstwowe zmontowane na terenie ogrodu

Uniwersytetu (fot. R. Motro)

Fig. 2. Two assembled double layer grids inside the University garden

(photo by R. Motro)

„Węzły i struktury przestrzenne” – w hołdzie Stefanowi du Château / “Nodes and Spatial Structures”, a tribute to Stéphane du Château 45

pro jek towane przez du Château dla trójkierunkowej

warst wy podwójnej wybudowanej w Nîmes niedaleko

auto strady.

Zasada projektowania wybrana przez niego jest podob-

na do rozwiązań dwukierunkowych przedstawionych po-

wyżej: rury są gniecione i przewiercane (warstwy dolne)

i w tym przypadku poszczególne elementy są zaprojekto-

wane dla elementów łączących warstwę dolną zaledwie

jedną śrubą. Na warstwie górnej siatka jest trójkątna i po-

trzebne są trzy śruby na każdym węźle (il. 3). Projekt wę-

zła musi brać pod uwagę nie tylko ﬁ zyczne występowanie

danego elementu, węzła, ale również wszystkich powią-

zanych ograniczeń, od uprzemysłowienia jego produkcji,

aż do zastosowania specjalnie przystosowanych narzędzi,

dla których trzeba pozostawić miejsce. „Otwory”, które są

widoczne w węzłach warstwy górnej, umożliwiają wpro-

wadzenie klucza do dokręcenia śrub.

• Węzeł kulisty – Spherobat

Mimo że Unibat był rozwiązaniem udanym, okazało

się, że realizacje Stefana du Château potrzebują innego

systemu węzłów i elementów, który będzie można ła-

twiej transportować niż piramidy. Na szczęście wszyscy

specjaliści w tamtych czasach znali skuteczne zastosowa-

nie tzw. węzła Mero, a w konkursie na projekt lotniska

w Baltimore (1975) amerykańscy architekci chętnie wy-

korzystali węzły kuliste. Stefan du Château zaprojektował

kulę z wierconymi otworami, w której mogły schodzić

się elementy. Po jakimś czasie badania nad węzłem ku-

listym umożliwiającym montaż elementów, bez względu

na ich wzajemne położenie, pozwoliły na zastosowanie

węzła kulistego, składającego się z dwóch części: jednej

stanowiącej jedną trzecią kuli i drugiej stanowiącej dwie

trzecie kuli.

Jeden osiowy łącznik jest wykorzystywany do po łą-

czenia dwóch części węzła. Śruby z łbem imbuso wym

służą do połączenia prętów z węzłem. Możliwe jest rów-

nież wykonanie prętów z końcówką stożkową (il. 4).

bottom layer with again only one bolt. On the upper layer,

the mesh is triangular and three bolts are necessary at each

node (Fig. 3). The node’s design must include not only the

physical existence of this speciﬁ c piece, the node, but also

all the surrounding constraints, from its industrialization

to their implementation by the use of adapted tools for

which it is necessary to make way. The “holes” that ap-

pear on the top layer are used to introduce the tools that

are applied to tighten the bolts.

• Spherical node – Spherobat

Even if Unibat was successful it appeared that du Châ-

teau’s realizations needed another system with nodes and

members, which are easier to transport than pyramids.

And all specialists knew the success of the so-called Mero

node in those years. Taking advantage of the contest for the

Baltimore airport (1975), American architects were will-

ing to use spherical nodes. Du Château designed a drilled

sphere that could receive the members. Some time after

the research for a spherical node enabling the assembly

of members whatever their relative positions, ends in

a spherical node assembled in two pieces: one is one third

of the sphere, the second one is two-thirds of the sphere.

One axial node is used to assemble the two pieces,

socket head cap screws are used to assemble the members

to the node itself. Conical rod end housings can also be

manufactured for some members (Fig. 4).

Industrialization and patents

Stéphane du Château patented many systems. Pyra-

mitec, Tridimatec, Unibat, Spherobat are some of them.

He is also the author of around two hundred and ﬁ fty

projects based on nodes’ patents. A comprehensive list

of these projects can be found in the thesis submitted by

Claudia Estrela Porto [5].

Three constraints governed the design:

– simple manufacturing in factory,

Il. 3. Sieć trójkierunkowa: a) węzeł warstwy dolnej, b) węzeł warstwy górnej (fot. R. Motro)

Fig. 3. Three directional grid: a) bottom layer “node”, b) top layer “node” (photo by R. Motro)

46 René Motro

Uprzemysłowienie i patenty

Stefan du Château opatentował wiele systemów kon-

strukcyjnych, np. Pyramitec, Tridimatec, Unibat czy też

Spherobat. Jest on również autorem około 250 projek-

tów opartych na opatentowanych węzłach. Wyczerpującą

listę tych projektów można znaleźć w pracy Claudii Es-

treli Porto [5].

Istniały trzy wymagania projektowe:

– prosta produkcja w fabryce,

– łatwy transport i składowanie (il. 5),

– uproszczony montaż.

W czasie całego procesu projektowego Stefan du Châ-

teau współpracował z Zygmuntem Stanisławem Makow-

skim, który wykonał analizy numeryczne jego struktur

oraz w niektórych przypadkach badania eksperymentalne.

Ta współpraca była bardzo owocna podczas prac i nnowa-

cyjnych.

Niestrudzony obrońca struktur przestrzennych

Stefan du Château pracował z najsłynniejszymi in ży-

nierami i architektami na całym świecie. Konsultował

się z nim np. Frei Otto w związku ze składaną membraną

w Cannes we Francji. Maszt, wykonany w tym obiekcie

– easy transport and storage (Fig. 5),

– simpliﬁ ed implementation.

All along his design process Stéphane du Château co-

worked with Zygmunt Stanisław Makowski, who made

numerical analyses of his structures and for some cases

experimental tests. This collaboration was very fruitful

during this period of innovation.

A tireless defender of spatial structures

Du Château worked with the most famous engineers and

architects in the whole world. He was consulted by Frei

Otto for a foldable membrane in Cannes, France (Fig. 6),

certainly one of the ﬁ rst foldable membrane projects. The

ﬁ rst central mast buckled and a new one was designed by

Stéphane du Château.

Founder of many associations, Stéphane du Château

tried to unify the action of French designers namely in his

IRASS (Institut de Recherche et d’Applications des Struc-

tures Spatiales) where famous engineers and architects

exchanged their ideas. Paul Maymont, Jean Cesselin (for

cable nets), Yona Friedman (architecture), Yves Chaperot

(polycorolles), Robert Lourdin (timber spatial structures)

were some of them. We organized together several events

in France in order to publicize spatial structures, namely

Il. 4. Spherobat

– zasada projektowania

(rys. S. du Château)

Fig. 4. Spherobat

– design prin ciple

(drawing by S. du Château)

końcówka pręta, aktualna/the end of the rod, current

/embout de barre courant

SPHEROBAT

śruba łącząca półkule/screw connecting hemispheres

/vis d’assemblage des calottes

duża półkula/large hemisphere/grande calotte

mała półkula

/small hemisphere/petit calotte

końcówka pręta, wariant/the end of the rod, variant

embout de barre, variante

śruba o wysokiej wytrzymałości z łbem imbusowym

/high strength socket head screw/vis 6 pans creux h.r

Il. 5. Komponenty przemysłowe: a) elementy warstwy dolnej, b) piramidki tworzące warstwę górną i środkową (fot. R. Motro)

Fig. 5. Industrialized components: a) elements of the bottom layer, b)pyramids composing the upper and middle layer (photo by R. Motro)

„Węzły i struktury przestrzenne” – w hołdzie Stefanowi du Château / “Nodes and Spatial Structures”, a tribute to Stéphane du Château 47

według pierwotnego projektu, uległ wyboczeniu i du Châ-

teau zaprojektował nowy (il. 6).

Założyciel wielu stowarzyszeń, Stefan du Château,

pró bo wał zjednoczyć działania francuskich projektan-

tów w swo im Instytucie IRASS (Institut de Recherche et

d’Appli cations des Structures Spatiales), gdzie wymie niali

poglądy znani inżynierowie i architekci, tacy jak Paul May-

mont, Jean Cesselin (konstrukcje cięgnowe), Yona Fried-

man (architektura), Yves Chaperot (polyco rolles), Robert

Lour din (drewniane struktury przestrzenne). Razem ze Ste -

fanem du Château zorganizowaliśmy kilka imprez we Fran -

cji (w Paryżu, Lyonie i Rennes) w celu spopularyzowa nia

struktur przestrzennych. Stefan zaprosił nawet do Paryża

Feliksa Candelę i był bardzo dumny z tego, że mógł go

uhonorować. Wszystkie regularne spotkania IRASS odby-

wały się w jego biurze Paryżu 15 rue Hégésippe Moreau.

Christel Frapier opisał niektóre z jego działań w pra-

cy opublikowanej przez „International Journal of Space

Structures” [6].

Grupa ta utrzymywała również kontakty z Robertem

Le Ricolais’m (il. 7). Ale on miał specyﬁ czną sytuację.

Niestety we Francji nie mógł on znaleźć niezbędnego

kontekstu merytorycznego ani wsparcia ﬁ nansowego dla

swoich badaczy i przeniósł się do Filadelﬁ i.

Robert Le Ricolais nie był w stanie dalej prowadzić

badań we Francji, mimo że wiele oddanych mu osób

próbowało mu pomóc, jednak z niewielkim sukcesem.

Na leży tutaj wspomnieć Davida Georges’a Emmericha

i je go próby powołania do życia Warszta tu Badań Struk-

turalnych, gdzie Le Ricolais mógłby kontynuować swoje

prace. Kiedy ostatni raz uczestni czył on w działaniach

tej grupy zagorzałych zwolenni ków (IRASS), tak o tym

mówił, w relacji Henri Drevona w styczniu 1977 r.:

Le Ricolais, który zabrał ze sobą dwóch swoich ucz-

niów, donosił o zadaniach, które były mu przy dziela ne

in Paris, Lyon and Rennes. He invited to Paris Felix Can-

dela, and was very proud to honor him. All the IRASS

regular meetings were held in his ofﬁ ce in Paris 15 rue

Hégésippe Moreau.

Christel Frapier described some of his activities in a pa -

per published by the “International Journal of Space Struc -

tures” [6].

This group was also maintained contacts with Robert Le

Ricolais (Fig. 7). But he had a speciﬁ c role. Unfortunately he

could not ﬁ nd the necessary context and the ﬁ nancial support

for his researches in France and migrated to Philadelphia.

Robert Le Ricolais was unable to further his research

in France, but many of his devotees endeavored to help

him to do so, unfortunately with little success. Reference

must be made here of the action of David Georges Emme -

rich who tried to set up a Structural Research Workshop

that could have welcomed Le Ricolais. The last time he

partici pated in this fervent group of followers (IRASS)

Il. 6. Od lewej: Stefan du Château i Frei Otto (archiwum S. du Château)

Fig. 6. From the left: Stéphane du Château and Frei Otto

(S. du Château archive)

Il. 7. „Zawsze wradzające się

na nowo w siebie” – Le Ricolais

(fot. R. Motro)

Fig. 7. “Always reborn

into itself” – Le Ricolais

(photo by R. Motro)

48 René Motro

he spoke in these terms, as related by Henri Drevon in

January 1977:

Le Ricolais, who had taken two of his students with

him, reported on the missions always assigned to him in

the USA. He regrets that the doctors do not allow him to

do more and that he has been unable to ﬁ nd an organiza-

tion in France that would enable him to pursue his task.

This entails, among other things, repatriating the impres-

sive set of models made with his students in Philadelphia,

which would put up a very good show in Pompidou Center.

Further he writes:

The proposal to honor Le Ricolais by transforming the

IRASS into a Le Ricolais Foundation is adopted unani-

mously and with an ovation [7].

It is not surprising that the so-called “IRASS” became

at the end the “Robert Le Ricolais Institute”.

Tireless propagator of spatial structures, Stéphane du

Château taught in many schools of architecture, increas-

ing the curiosity of young people, organized several scien-

tiﬁ c meetings. I had the chance to share these experiences

with him [8].

Consequently I asked him to be the honorary chairman

of a scientiﬁ c seminar on structural morphology that I or-

ganized in the south of France (Fig. 8) [9]. It was simulta-

neously possible to organize two exhibitions one devoted

to Ro bert Le Ricolais, and one to his close friend Stéphane

du Château. In both cases we could exhibit models from

their projects and studies.

Conclusion

Stéphane du Château was undoubtedly one of the

leaders in the ﬁ eld of space structures during the second

half of the 20

century. Designer, architect, space struc-

tures defender, teacher, he was a multiple expertise man.

I had the honor and privilege to work with him in many

circumstances and had the opportunity to discover his

deep humanity.

I also received a wonderful collection of slides from

his nephew, and my task is now to give access to this

collection, and to coordinate my action with Polish people

in charge of his foundation in Hrubieszów.

w USA. Żałuje on, że lekarze nie pozwalają mu więcej

pracować i że nie może znaleźć organizacji we Francji,

która umożliwiłaby mu realizację tego zadania. Wiąże się

to m.in. z przywiezieniem („repatriacją”) wspaniałych

modeli wykonanych z jego uczniami w Filadelﬁ i, co umoż-

liwiłoby zorganizowanie wspaniałej wystawy w Centrum

Pompidou.

Dalej pisze, że:

Propozycja uhonorowania Le Ricolais’go poprzez

przekształcenie IRASS w Le Ricolais Foundation została

owacyjnie i jednogłośnie przyjęta [7].

Nie jest niczym dziwnym, że tak zwany „Instytut

IRASS” stał się w końcu „Instytutem Roberta Le Rico-

lais’go”.

Niestrudzony propagator struktur przestrzennych, Ste-

fan du Château, uczył w wielu szkołach architektury, roz-

budzając zainteresowanie wśród młodych ludzi, i organi-

zował spotkania naukowe. Miałem szansę razem z nim

uczestniczy

ć w takich wydarzeniach [8].

W związku z tym poprosiłem go, aby został honoro-

wym prezesem seminarium naukowego na temat morfolo-

gii strukturalnej, które zorganizowałem na południu Fran-

cji (il. 8) [9]. Jednocześnie możliwe było zorganizowanie

dwóch wystaw, jednej poświęconej Robertowi Le Rico-

lais’mu, a drugiej jego bliskiemu przyjacielowi Stefano-

wi du Château. W obu przypadkach zaprezentowaliśmy

modele ich projektów i badań.

Podsumowanie

Stefan du Château był niewątpliwie jednym z lide rów

w dziedzinie struktur przestrzennych w 2. poł. XX w.

Był projektantem, architektem, obrońcą struktur prze-

strzennych, nauczycielem, człowiekiem o wielkiej facho -

wej wie dzy. Miałem honor i przywilej pracowania

z nim w wie lu różnych okolicznościach, a także oka-

zję do pozna nia jego charakteru, który cechuje jego głę-

boki hu ma nizm.

Ponadto otrzymałem od jego siostrzeńca wspaniały

zbiór slajdów i teraz stoi przede mną zadanie udostępnie-

nia tej kolekcji szerszej publiczności oraz skoordynowania

moich działań z działaniami Polaków pracujących w Fun-

dacji Krystyny i Stefana Du Château w Hrubieszowie.

Tłumaczenie

Tadeusz Szałamacha

Il. 8. Okładka katalogu wystawy z 1992 r.

Fig. 8. S. du Château Exhibition Catalog 1992

„Węzły i struktury przestrzenne” – w hołdzie Stefanowi du Château / “Nodes and Spatial Structures”, a tribute to Stéphane du Château 49

Streszczenie

Twórczość Stefana du Château jest wyraźnie wpisana w rozwój myśli architektonicznej 2. poł. XX w. Opracował on kilka systemów struktur

przestrzennych w oparciu o pomysłowy projekt węzłów, które wszystkie zostały opatentowane. Pona d 250 jego projektów zostało w pełni

zrealizowanych. Opr ócz tego Stefan du Château założył kilka stowarzyszeń, aby przyciągnąć projektantów i popularyzować struktury przestrzenne.

Jego charyzma i zaangażowanie były kluczem do niebywałego rozwoju struktur przestrzennych. Ten artykuł jest krótkim podsumowaniem oraz

przypomnieniem jego osiągnięć i ic h znaczenia dla rozwoju konstrukcji przestrzennych.

Słowa kluczowe: struktury przestrzenne, Stefan du Château, węzeł, uprzemysłowienie, Institut Le Rico lais

Abstract

The work of Stéphane du Château is clearly inscribed in the second half of the 20

century. He developed several spatial structures’ systems based

on a clever design of nodes, which were all patented. More than two hundred and fifty projects were effectively built. Besides this productive work

Stéphane du Château founded several associations in order to gather designers and to promote Spatial Structures. His charisma and his commitment

were the keys of a remarkable contribution to spatial structures. This paper is a short summary and a reminder of his achievements and importance

for the development of spatial structures.

Key words: spatial structures, Stéphane du Château, node, industrialisation, Institut Le Ricolais

Bibliografia /References

[1] Du Château S., L’intégration de la pensée technique dans la créa-

tion architecturale, [w:] R.M. Davies (ed.), Proceedings of the First

International Conference on Space Structures, Blackwell Scientiﬁ c

Publications, London 1966, 1180–1198.

[2] Barucki T., Stéphane du Château, Kanon, Warszawa 1995.

[3] Motro R., Optimisation de Structures Spatiales et application à des

grilles à double nappe (2 vol.), Thèse de Docteur Ingénieur. Univer-

sité Paul Sabatier, Toulouse 1975.

[4] Motro R. (ed.), Colloque Recherches en Structures: Bilan et Pers-

pectives, Université Montpellier II, Montpellier 1976.

[5] Estrela Porto C., L’évolution des Structures Spatiales à travers

l’œuvre de Stéphane du Château, Thèse Université Paris 1, Paris 1993.

[6] Frapier C., Stéphane du Château, „International Journal of Space

Structures” (Special Issue The pioneers of Space Structures), 2006,

Vol. 21, No. 1, 53–59.

[7] Unpublished report of IRASS meeting. Personal correspondence

between H. Drevon and R. Motro.

[8] Motro R., Wester T., Proceedings of the ﬁ rst International Seminar

on Structural Morphology, Montpellier 1992.

[9] Motro R. (ed.), Structural Morphology by R. Le Ricolais and S. du

Château, Katalog wystawy/Catalog of the exhibition, Montpellier

199 2.

Nowe tereny targowe Nuova Fiera di Roma

w Rzymie – główne wejście z przekryciem

membranowym ze stali nierdzewnej

nad kładką dla pieszych o długości 1,8 km

(arch. T. Valle, konstr. M. Majowiecki)

(fot. M. Majowiecki)

New market areas, Nuova Fiera di Roma,

in Rome – main entrance with a membrane

covering made of stainless steel above the foot-

bridge of 1.8 km in lenght (arch. T. Valle,

structural engineer

M. Majowiecki)

(photo by M. Majowiecki)